If ΔABCandΔDBC are on the same base BC, AB = DC and AC = DB (Fig. 6.21), then which of the following gives a congruence relationship?
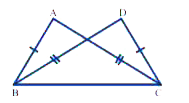
ΔABC≅ΔDBC
ΔABC≅ΔCBD
ΔABC≅ΔDCB
ΔABC≅ΔBCD
The correct Answer is:C
Step by step video, text & image solution for If ∆ABC and ∆DBC are on the same base BC, AB = DC and AC = DB (Fig. 6.21), then which of the following gives a congruence relationship? by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - Match the following
2 Videos
- CONGRUENCE OF TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - Assertion & Reaction Type
5 Videos
- CONGRUENCE OF TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - NCERT Section (Exercise 7.2)
20 Videos
- COMPARING QUANTITIES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - COMPARING QUANTITIES EXERCISE - Olympaid/HOTS Corner
20 Videos
- DATA HANDLINGBOOK - MTG IIT JEE FOUNDATIONCHAPTER - DATA HANDLINGEXERCISE - Olympiad / Hots Corner
20 Videos
Similar Questions
Knowledge Check
In △ABCand△PQR If AB = QP ,∠B=∠P, BC=PR then which one of the following congruence conditions applies :
ASASBASACSSSDRHS
Triangles ABC and DBC have side BC common, AB=BD and AC=CD. Are the two triangles congruent? State in symbolic form. Which congruence condition do you use? Does △ABD equal △ACD? Why or why not?
View SolutionTwo triangles ABC and DBC are on the same base BC and on the same side of BC in which ∠A=∠D=90∘. If CAandBD meet each other at E, show that AE.EC=BE.ED.
View SolutionIn Figure, ABC and DBC are two triangles on the same base BC such that AB=AC and DB=DC. Prove that ∠ABD=∠ACD
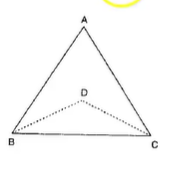
View SolutionABC and DBC are two triangle on the same base BC such that A and D lie on the opposite sides of BC,AB=AC and DB =DC ,Show that AD is the perpedicular bisector of BC.
View SolutionΔABCandΔDBC are on same base BC and their vertices A and D are on opposite sides of BC. It is given that:
area of ΔABC= area of ΔDBC
Prove that BC bisects the line segment AD.
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E show that
View SolutionABC and DBC are both isosceles triangles on a common base BC such that A and D lie on the same side of BC. Are triangles ADB and ADC congruent? Which condition do you use? If ∠BAC=400 and ∠BDC =1000; then find ∠ADB
View Solution