If denote the area of any triangle with semi-perimeter , then
To solve the problem, we need to establish the relationship between the area of a triangle (Δ) and its semi-perimeter (s). The semi-perimeter s is defined as:
s=a+b+c2
where a,b,c are the lengths of the sides of the triangle. We will use the formula for the area of a triangle in terms of its semi-perimeter and its sides, known as Heron's formula, which states:
Δ=√s(s−a)(s−b)(s−c)
1. Define the semi-perimeter:
s=a+b+c2
2. Use Heron's formula for the area:
Δ=√s(s−a)(s−b)(s−c)
3. Express the terms s−a,s−b,s−c:
s−a=b+c−a2,s−b=a+c−b2,s−c=a+b−c2
4. Substitute these into Heron's formula:
Δ=√s⋅b+c−a2⋅a+c−b2⋅a+b−c2
5. Simplify the expression:
Δ=√s(b+c−a)(a+c−b)(a+b−c)8
6. Establish inequalities using the AM-GM inequality:
By applying the AM-GM inequality:
s+(s−a)+(s−b)+(s−c)4≥√(4)s(s−a)(s−b)(s−c)
This implies:
s≥√(4)s(s−a)(s−b)(s−c)
7. Square both sides:
s2≥√s(s−a)(s−b)(s−c)
8. Use the derived inequalities:
From the previous steps, we can derive:
Δ2≤s24
9. Final conclusion:
Thus, we can conclude:
Δ<s24
Final Result:
The area of the triangle Δ is less than s24.
s=a+b+c2
Δ=√s(s−a)(s−b)(s−c)
s−a=b+c−a2,s−b=a+c−b2,s−c=a+b−c2
Δ=√s⋅b+c−a2⋅a+c−b2⋅a+b−c2
Δ=√s(b+c−a)(a+c−b)(a+b−c)8
By applying the AM-GM inequality:
s+(s−a)+(s−b)+(s−c)4≥√(4)s(s−a)(s−b)(s−c)
This implies:
s≥√(4)s(s−a)(s−b)(s−c)
s2≥√s(s−a)(s−b)(s−c)
From the previous steps, we can derive:
Δ2≤s24
Thus, we can conclude:
Δ<s24
The area of the triangle Δ is less than s24.
Topper's Solved these Questions
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - SOLVED MCQ
2 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Section II - Assertion Reason Type
13 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test
55 Videos
- PLANE AND STRAIGHT LINE IN SPACE BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test
31 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test
58 Videos
Similar Questions
Knowledge Check
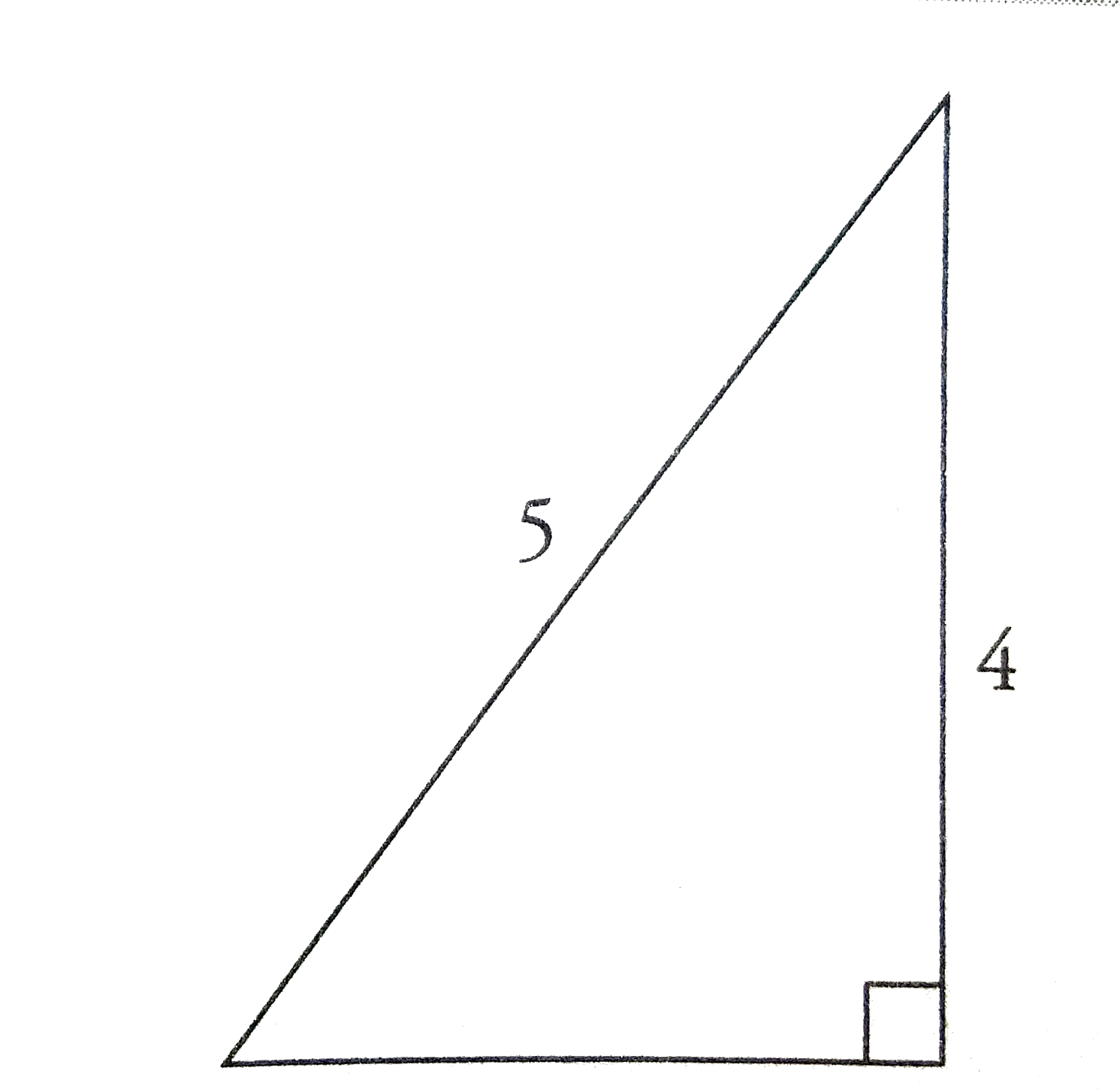
If the area of the triangle above is 6, what is its perimeter?A11B12C15D16
If the area os a triangle is 81 square cm and its perimeter is 27 cm, then find its in-radius in centi-metres.
View SolutionIf the difference between the two sides of a right-angled triangle is 2 cm and the area of the triangle is 24cm2 , find the perimeter of the triangle.
View SolutionLet a,b,c be the sides of triangle whose perimeter is P and area is A, then
View SolutionThe length of the sides of a triangle are in the ratio 3:4:5. Find the area of the triangle if its perimeter is 144 cm.
View SolutionConsider a right triangle with legs of length a and b and hypotenuse of lengthc. If k denotes the area of the triangle then the value of (a+b) equals
View SolutionFind the altitude and area of an isosceles triangle whose perimeter is 64 cm and whose base is 24 cm.
View SolutionFind the altitude and area of an isosceles triangle whose perimeter is 64 cm and where base is 2 cm.
View Solution
