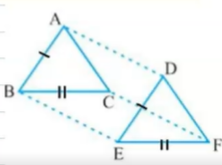
If Figure, arms BAandBC OF ∠ABC are respectively parallel to arms ED andEF or ∠DEF . Prove that ∠ABC=∠DEF
Given: In '∠ABC'and'∠DEF''BA||ED'and'BC||EF'<br>Toprove:∠ABC+∠DEF=180∘'
Construction : Produce 'BC' to 'H' intersecting 'ED' at 'G'
Proof:
∵'AB || ED'
∴'∠ABC=∠EGH'...(i) (Corresponding angles)
∵'∠EGH+∠DEF=180∘ (Sum of co-interior angles)
⇒∠ABC+∠DEF=180∘[From(i)]
Hence proved.
Topper's Solved these Questions
Similar Questions
If Figure, arms BAandBC OF ∠ABC are respectively parallel to arms ED andEF or ∠DEF . Prove that ∠ABC=∠DEF
View SolutionIn Figure, arms BAandBCof∠ABC are respectively parallel to arms ED and EF of ∠DEF. Prove that ∠ABC+∠DEF=180∘
View SolutionIf ABC and DEF are two triangles such that AB, BC are respectively equal and parallel to DE, EF, then show that Quadrilateral ABED is a parallelogram Quadrilateral BCFE is a parallelogram AC=DF (iv) ABC ≅ DEF
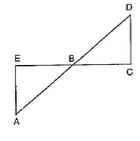
View SolutionIn Figure, ∠E>∠A and ∠C>∠D . Prove that AD>EC
View SolutionIn Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD

View SolutionIn Figure, AB and CD are respectively the smalles and longest sides of a quadrilateral ABCD. Show that ∠A>∠C and ∠B>∠D.

View SolutionIn Figure, AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD. Show that ∠A>∠C and ∠B>∠D
View SolutionIn Fig. 4.102 (i) and (ii) , if CD and GH (D and H lie on AB and FE ) are respectively bisectors of ∠ACB and ∠EGF and ABC~FEG , prove that (FIGURE) DCA~HGF (ii) CDGH=ACFG (iii) DCB~HGE
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ

View SolutionIn Figure, ABCD, ABFE and CDEF are parallelograms. Prove that ar(ADE)=ar(BCF)
View Solution
