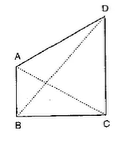
In Figure, AB
and CD are respectively the smalles and longest
sides of a quadrilateral ABCD.
Show that ∠A>∠C
and ∠B>∠D.

Step by step video & image solution for In Figure, A B and CD are respectively the smalles and longest sides of a quadrilateral A B C Ddot Show that /_A >/_C and /_B >/_Ddot by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In a cyclic quadrilateral ABCD∠A+∠B+∠C+∠D=?
AA)90∘BB)360∘CC)180∘DD)120∘
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see th e given figure). Show that ∠A>∠C and ∠B>∠D
 View Solution
View SolutionIn figure OA∗OB=OC∗OD. Show that ∠A=∠Cand ∠B=∠D.
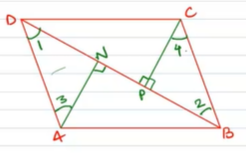
View SolutionIn Figure, AN and CP are perpendicular to the diagonal BD of a parallelogram ABCD. Prove that : ADN≅CBP (ii) AN=CP
 View Solution
View SolutionIf ABCD is a quadrilateral in which ABCD and AD=BC, prove that ∠A =∠B.
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionE,F,G,H are respectively, the mid-points of the sides AB,BC,CD and DA of parallelogram ABCD . Show that the quadrilateral EFGH is a parallelogram and that its area is half the area of the parallelogram, ABCD. GIVEN : A quadrilateral ABCD in which L,F,G,H are respectively the mid-points of the sides AB,BC,CD and DA. TO PROVE : (i) Quadrilateral EFGH is a parallelogram ar(^(gm)EFGH)=12ar(^(gm)ABCD) CONSTRUCTION : Join AC and HF
View SolutionIn ABC, if ∠A=400and ∠B=600. Determine the longest and shortest sides of the triangle.
View Solution