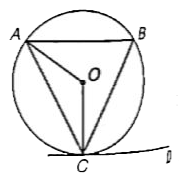
If figure, O is the centre of the circle, BD=ODandCD⊥AB. Find∠CAB.

Video Solution
Text Solution
Given, in the figureBD=OD,CD⊥AB.
In ΔOBD,BD=OD [given]
OD=OB [both are the radius of circle]
∴OB=OD=BD

Thus, ΔODB is an equilateral triangle.
∴∠BOD=∠OBD=∠ODB=60∘
In ΔMBCandΔMBD,MB=MB [common side]
∠CMB=∠BMD=90∘
and CM=MD
[ in a circle, any perpendicular drawn on a chord also bisects the chord]
∴ΔMBC≅ΔMBD [by SAS congruence rule]
∴∠MBC=∠MBD [by CPCT]
⇒∠MBC=∠OBD=60∘[∴∠OBD=60∘]
since, AB is a diameter of the circle.
∴∠ACB=90∘
In ΔACB,∠CAB+∠CBA+∠ACB=180∘
by angle sum property of a triangle]
⇒∠CAB+60∘+90∘=180∘
⇒∠CAB=180∘−(60∘+90∘)=30∘
|
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
Knowledge Check
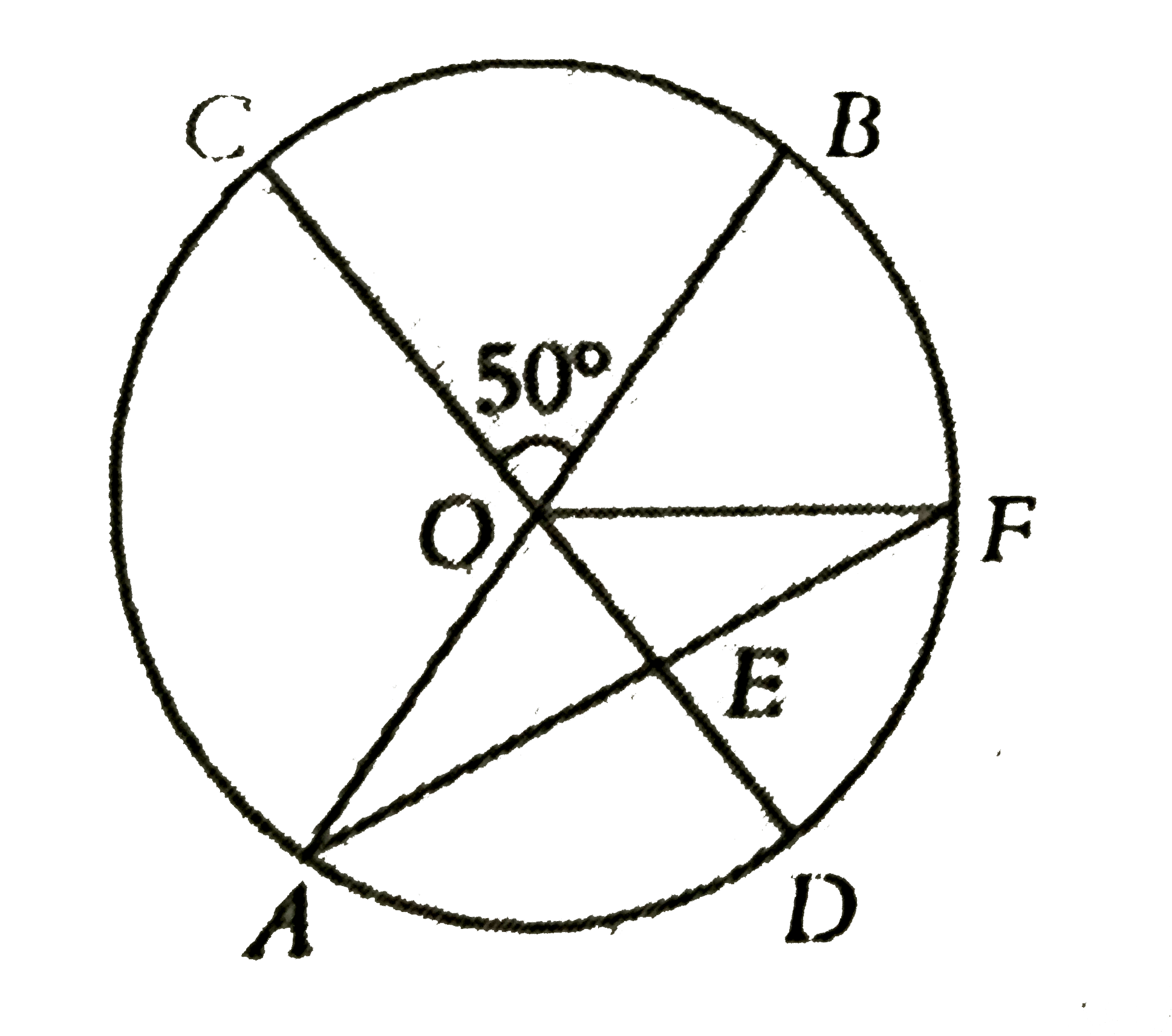
In the above figure , O is the centre of the circle, AB and CD are diameters. ∠COB=50∘=50∘ . If E is the midpoint of AF, then find ∠ADFA130∘B100∘C110∘D120∘
In the above figure, O is the centre of the circle and AB=CD. If ∠APB=110∘, then find the angle made by the chord CD at the centre.A220∘B110∘C120∘D140∘In the given figure, AB is the diameter of the circle, ∠ADC=120∘. Find ∠CAB:
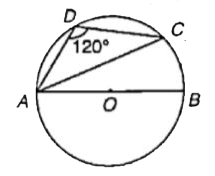 A20∘B30∘C40∘Dcan't be determined
A20∘B30∘C40∘Dcan't be determined

In the above figure , O is the centre of the circle, AB and CD are diameters. ∠COB=50∘=50∘ . If E is the midpoint of AF, then find ∠ADF
View Solution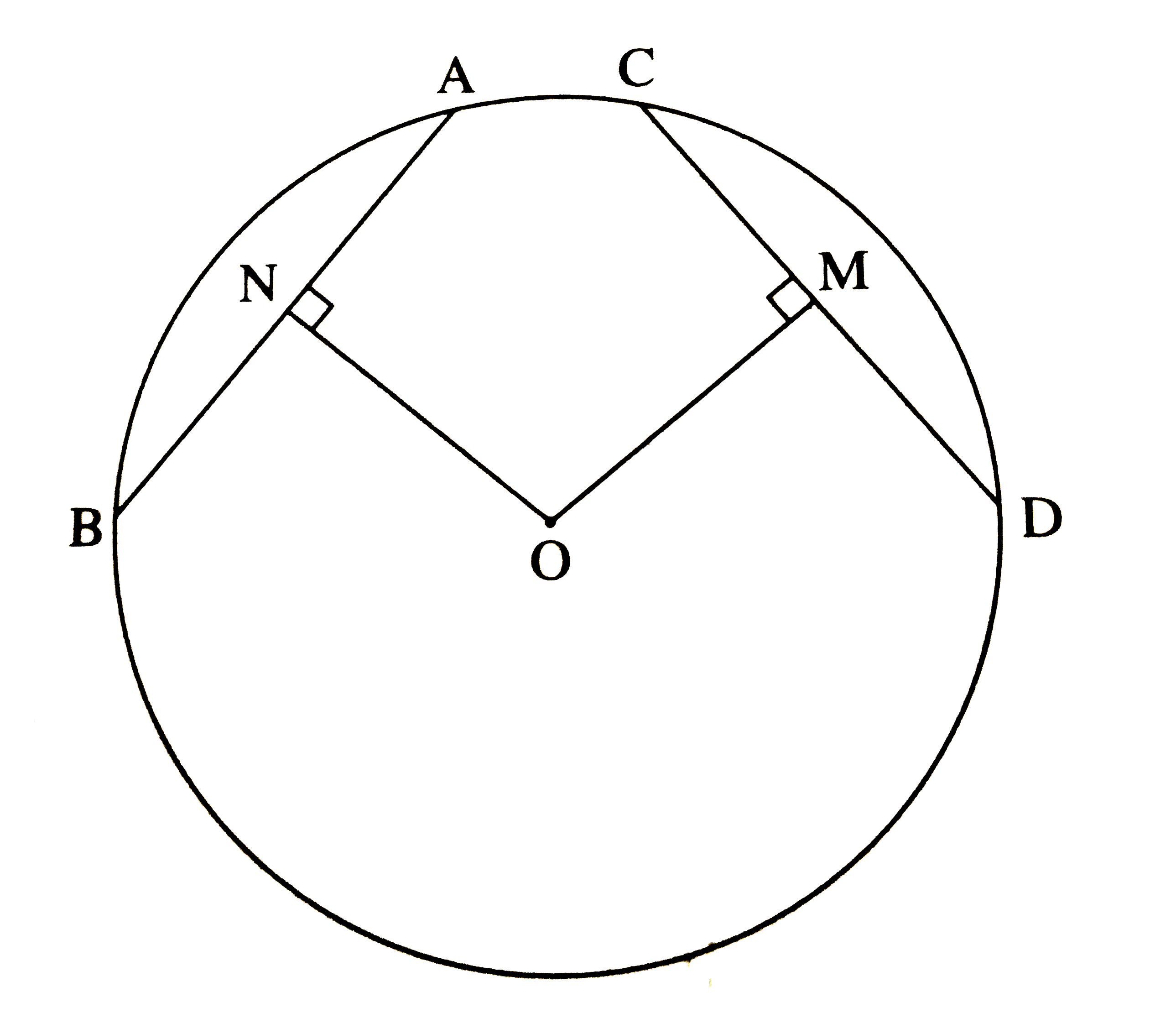
In the figure , O is the center of the circle.chord AB and CD are congruent . If seg ON ⊥ chord AB and seg OM ⊥ chord CD and OM =4cm , then find ON . Justify your answer .
View SolutionIn the given figure O is the centre of the circle and AB||CD. If ∠ADC=25∘, then find ∠AEB∘-

View SolutionIn the given diagram O is the centre of the circle and CD is a tangent. ∠CABand∠ACD are supplementary to each other , ∠OAC=30∘. Find the value of ∠OCB :
View Solution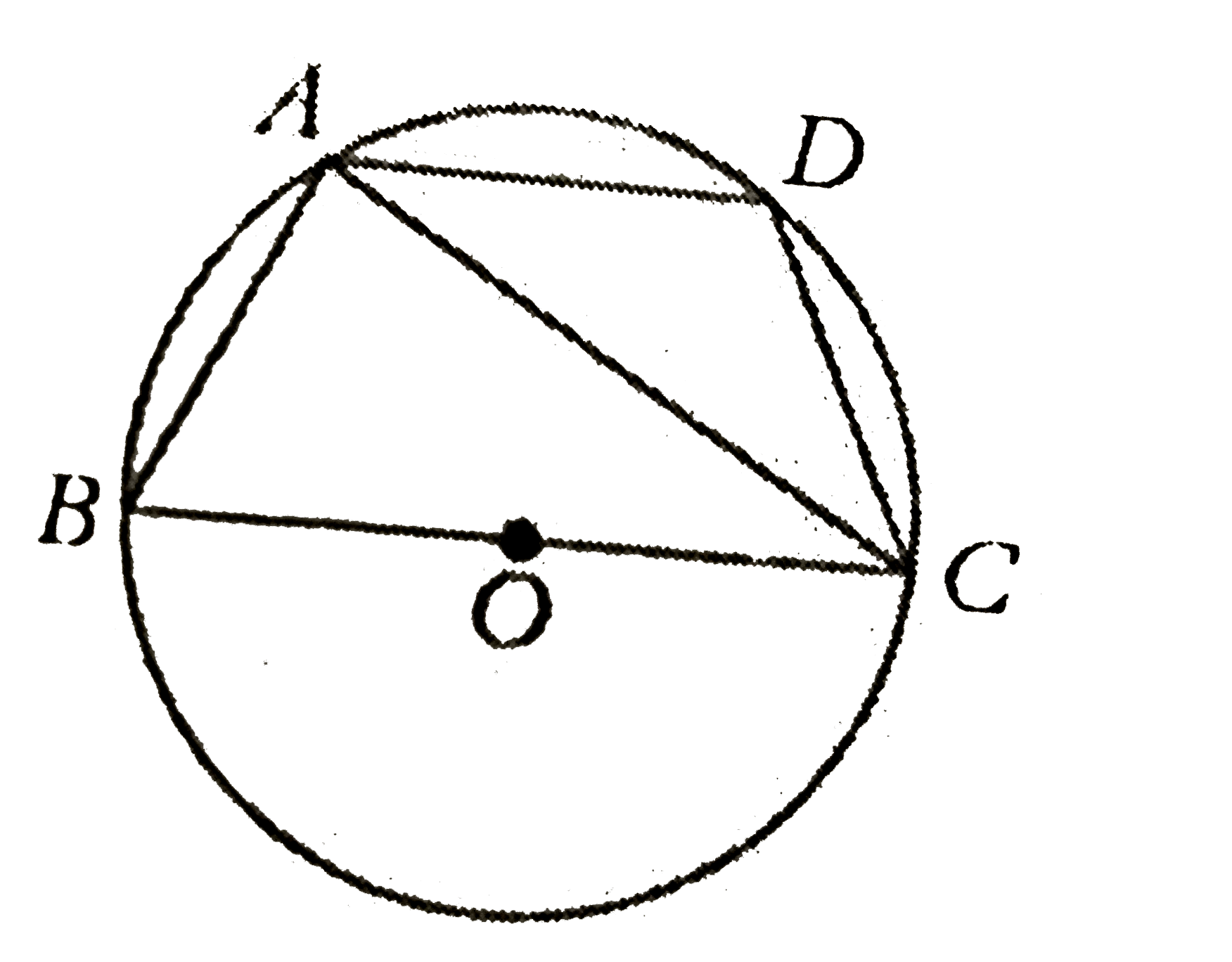
In the above figure, O is the centre of the circle AB,AD and CD are the chords . If ∠ADC=130∘ then fid ∠ACB.
View Solution

