If f''(x)+f'(x)+f2(x)=x2 is the differential equation of a curve and let P be the point of maxima, then number of tangents which can be drawn from P to
x2−y2=a2 is/areSolution in Punjabi
The correct Answer is:2
Step by step video solution for If f''(x)+f'(x)+f^(2)(x)=x^(2) is the differential equation of a curve and let P be the point of maxima, then number of tangents which can be drawn from P to x^(2)-y^(2)=a^(2) is/are by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MONOTONICITY MAXIMA AND MINIMABOOK - ARIHANT MATHSCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - MAXIMA AND MINIMA EXERCISE 6
2 Videos
- MONOTONICITY MAXIMA AND MINIMABOOK - ARIHANT MATHSCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
31 Videos
- MONOTONICITY MAXIMA AND MINIMABOOK - ARIHANT MATHSCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - MAXIMA AND MINIMA EXERCISE 5
4 Videos
- MATRICES BOOK - ARIHANT MATHSCHAPTER - MATRICES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
49 Videos
- PAIR OF STRAIGHT LINES BOOK - ARIHANT MATHSCHAPTER - PAIR OF STRAIGHT LINES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
2 Videos
Similar Questions
The figure shows a right triangle with its hypotenuse OB along the y-axis and its vertex A on the parabola y=x2.
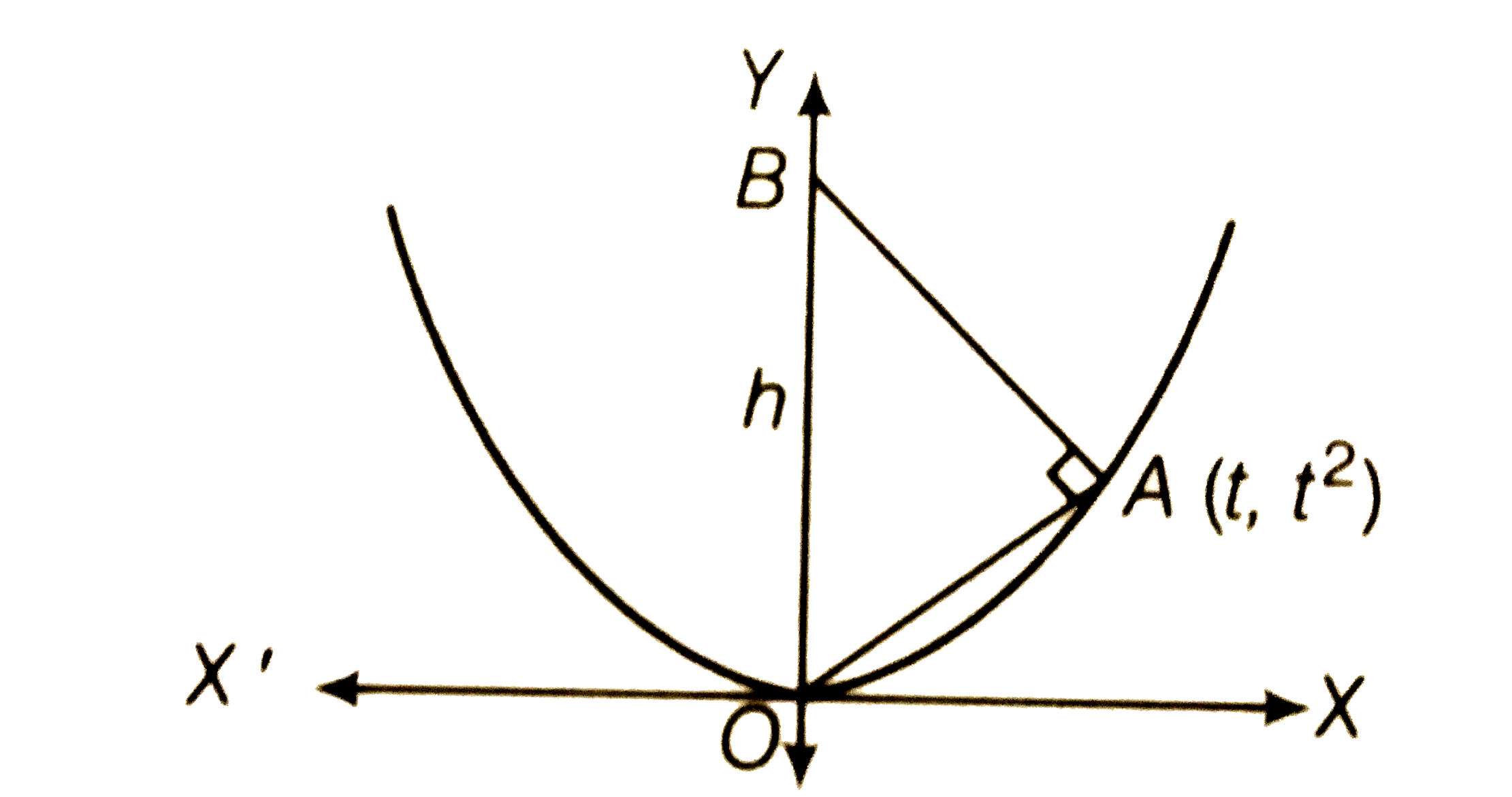
Let h represents the length of the hypotenuse which depends on the x-coordinate of the point A. The value of limt→o(h) is equal to
View SolutionThe least value of α∈R for which 4ax2+1x≥1, for all x>0, is
View SolutionEvaluate ∫(sinx+2cosx)dx.
View SolutionLet A=⎡⎢⎣1000110−24⎤⎥⎦,I=⎡⎢⎣100010001⎤⎥⎦andA−1=[16(A2+cA+dI)] Then value of candd are (a) (−6,−11) (b) (6,11) (c) (−6,11) (d) (6,−11)
View SolutionIf the pair of lines ax2+2(a+b)xy+by2=0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then
View SolutionIf 9+f(x)+f'(x)=x^(2)+f^(2)(x) be the differential equation of a curve and let P be the point of minima of this curve then the number of tangents which can be drawn from P to the circle x^(2)+y^(2)=8 is
View SolutionIf 9+f(x)+f'(x)=x^(2)+f^(2)(x) be the differential equation of a curve and let P be the point of minima of this curve then the number of tangents which can be drawn from P to the circle x^(2)+y^(2)=8 is
View SolutionConsider f(x)=∫x1(t+1t)dt and g(x)=f'(x) If P is a point on the curve y=g(x) such that the tangent to this curve at P is parallel to the chord joining the point (12,g(12)) and (3,g(3)) of the curve then the coordinates of the point P
View SolutionDetermine a differentiable function y = f(x) which satisfies f (x)=[f(x)]2 and f (0)= −12. Find also the equation of the tangent at the point where the curve crosses the y-axis .
View SolutionA curve f(x)=x2+ax−b pass through p(1,−5) and tangent to f(x) at point p is perpendicular to x−y+5=0 then which of the following point will lie on curve ?
View SolutionLet f(x)=sinx−tanx,x∈(0,π/2) then tangent drawn to the curve y=f(x) at any point will
View SolutionIf f''(x)+f'(x)+f2(x)=x2 be the differentiable equation of a curve and let p be the point of maxima then number of tangents which can be drawn from p to x2−y2=a2 is/are……. .
View SolutionThe curve y=f(x) in the first quadrant is such that the y - intercept of the tangent drawn at any point P is equal to twice the ordinate of P If y=f(x) passes through Q(2,3), then the equation of the curve is
View SolutionIf the straight line y=x meets y=f(x) at P, where f(x) is a solution of the differential equation dydx=x2+xyx2+y2 such that f(1)=3, then the value of f'(x) at the point P is
View SolutionIf 9+f"(x)+f'(x)=x2+f2(x) where f(x) is twice differentiable function such that f''(x)≠0∀x∈R and P be the point of maxima of f(x) , then find the number of tangents which can be drawn from P to the circle x2+y2=9
View Solutionमाना y=f(x) एक अवकलनीय फलन है जो f’(x)=f2(x) को संतुष्ट करता है तथा f(0)=−12 है। अवकलनीय पुलन y=g(x) के आरेख पर कोई बिंदु (0,2) है तथा उसका गुणधर्म है कि प्रत्येक संख्या P के लिए वक्र y=g(x) के बिंदु (P,g(P)) पर स्पर्श रेखा x- अक्ष x- अक्ष को P+2 पर प्रतिच्छेद करती है।
वक्र y=f(x),y− अक्ष को जिस बिंदु पर काटता है उस बिंदु पर स्पर्श रेखा की समीकरण है
View Solution
