Doubtnut Promotions Sticky

If f(x)=∫x0et2(t−2)(t−3)dt for all x∈(0,∞)
then which of the following is incorrect ?

A

f has a local maximum at x=2 and local minimum at x=3

B

f is dereasing on (2,3)

C

there exists c∈(0,∞) such that f (c)=0

D

f is inceresing on R+

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:D

We have
f(x)=x∫0e62(t−2)(t−3)dt
⇒f(x)=ex2(x−2)(x−3)
The chages in sings of f(x) for different values of x are as given below :
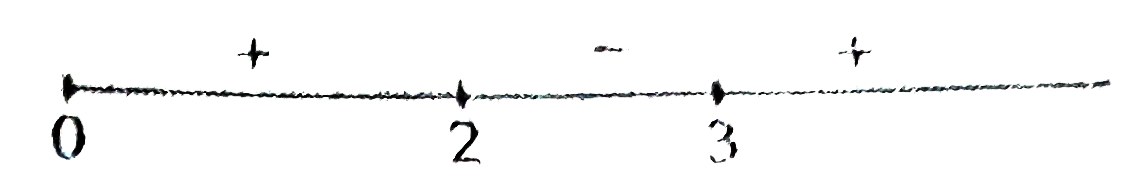
ocr_image
Clearly f(x)>0 for x∈(0,2)∪(3,∞) and f(x) lt 0 for(x)<0
x∈(2,3) So f(x) is increasing on (0,2)∪(3,∞) and decreasing on (2,3).
As f(x) changes sign from positive as x passes through 2 and negatives to positive as x passes through 3. So, x=2 is point of local maximum and x=3 is a point of local minmum of f(x).
Clearly f(x)=ex2(x−2)(x−3) is continuous on [2,3] and differentiable on (2,3).Also f(2)=f(3)=0 .Therefore by Rolle's theorem there exists c∈(2,3) such that f''(c) =0

|
Updated on:21/07/2023
Class 12MATHSAPPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One or More

    Let f:[0,∞)→R be a continuous function such that f(x)=1−2x+∫x0ex−tf(t)dt for all x∈[0,∞). Then, which of the following statements(s) is (are)) TRUE?

    AThe curve y=f(x) passes through the point (1,2)
    BThe curve y=f(x) passes through the point (2,-1)
    CThe area of the region {(x,y)∈[0,1]×R:f(x)≤y≤√1−x2} is π−24
    DThe area of the region {(x,y)∈[0,1]×R:f(x)≤y≤√1−x2} is π−14
  • Question 2 - Select One or More

    If f(x)=∫x0t2(t−2)(t−3)dtfor x∈[0,∞] then

    Af has a local maximum at x= 2
    Bf is decreasing on [2,3]
    C∃ some c∈]0,∞ such that f'(c)=0
    Df has a local minimum at x = 3
  • Question 3 - Select One

    if f(x)=∫x0(t2+2t+2) dt where x∈[2,4] then

    Athe minimum value of f(x) is 323
    Bthe minimum value of f(x)Is 10
    Cthe maxium value of f(x) is 10
    Dnone of these