Question

If $f\left(x\right)=x^3+4x^2+\lambda x+1$
is a monotonically decreasing function of $x$
in the largest possible interval $(-2,-\frac{2}{3})\stackrel{.}{}$
Then
$\lambda =4$
(b) $\lambda =2$

$\lambda =-1$
(d) $\lambda$
has no real value

Explanation

Here `f'(x) le 0`
`rArr" "3x^(2)+ 8x + lamda0 AA x in (-2, -(2)/(3))`
Then the situations for `f'(x)` are as follows :

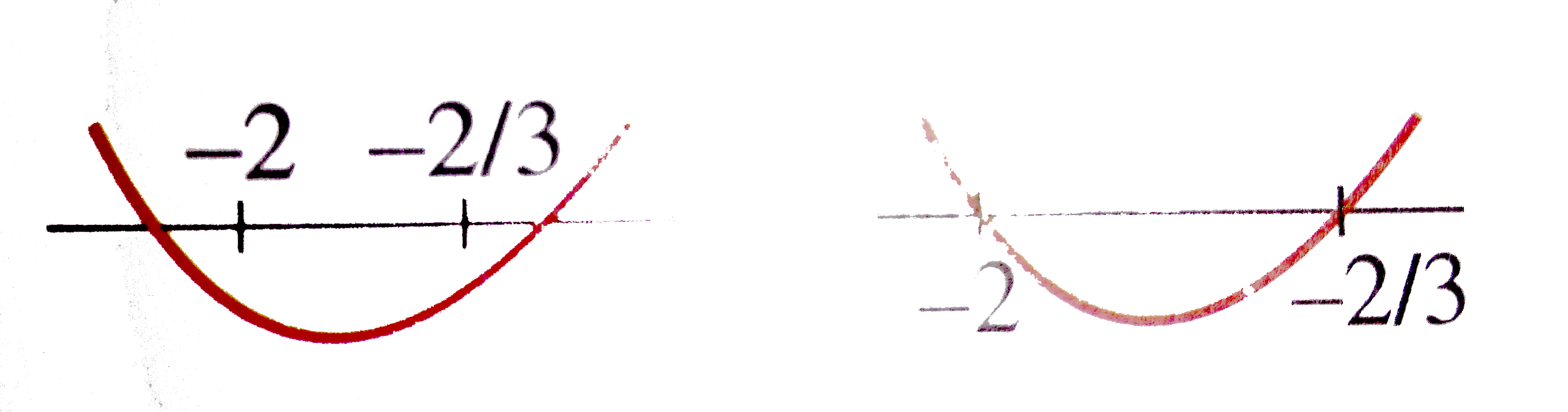
Given that `f(x)` decreases in the largest possible interval `(-2, -(2)/(3))`, then `f'(x)=0` must have roots -2 and `-2//3`.
So the product of the roots is `(-2)(-(2)/(3))= (lamda)/(3) rArr lamda=4`.