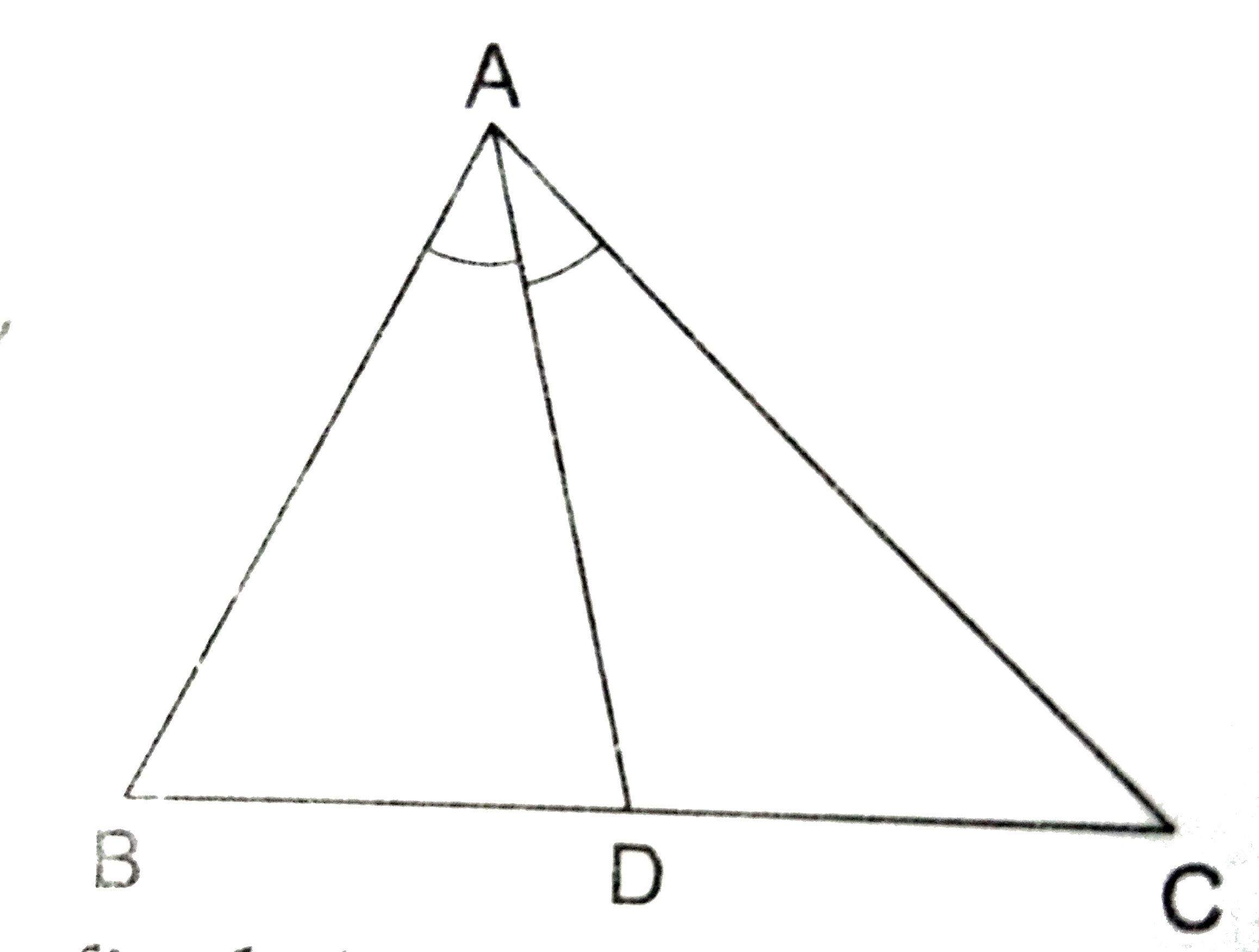
If in △ABC, AD is the bisector of ∠AandD lies on BC. If AB = 6.4 cm, AC = 8 cm, BD = 5.6 cm, find DC.
The correct Answer is:7 cm
To solve the problem, we will use the Angle Bisector Theorem, which states that the ratio of the two segments created by the angle bisector on the opposite side is equal to the ratio of the other two sides of the triangle.
1. Identify Given Values:
- AB=6.4cm
- AC=8cm
- BD=5.6cm
- Let DC=xcm
2. Apply the Angle Bisector Theorem:
According to the Angle Bisector Theorem:
ABAC=BDDC
Substituting the known values:
6.48=5.6x
3. Cross Multiply:
Cross multiplying gives us:
6.4⋅x=8⋅5.6
4. Calculate 8⋅5.6:
8⋅5.6=44.8
So, we have:
6.4x=44.8
5. Solve for x:
Divide both sides by 6.4:
x=44.86.4
6. Calculate 44.86.4:
x=7cm
7. Conclusion:
Therefore, DC=7cm.
Final Answer:
DC=7cm
- AB=6.4cm
- AC=8cm
- BD=5.6cm
- Let DC=xcm
According to the Angle Bisector Theorem:
ABAC=BDDC
Substituting the known values:
6.48=5.6x
Cross multiplying gives us:
6.4⋅x=8⋅5.6
8⋅5.6=44.8
So, we have:
6.4x=44.8
Divide both sides by 6.4:
x=44.86.4
x=7cm
Therefore, DC=7cm.
DC=7cm
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Revision Exercise Short Questions
10 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Revision Exercise Long Questions
4 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6d
24 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
In a ΔABC,AD is the bisector of ∠A.
(i) If AB=6.4cm,AC=8cmandBD=5.6cm, find DC.
(ii) If AB=10cm,AC=14cmandBC=6cm, find BD and DC.
(iii) If AB=5.6cm,BD=3.2cm,andBC=6cm, find AC.
(iv) If AB=5.6cm,AC=4cm,andDC3cm, find BC.
View SolutionIn the given figure AD is the bisector of ∠A. If BD= 4 cm , DC = 3 cm and AB = 6cm . Find AC.

View Solution
Knowledge Check
In the given figure , if AD is the bisector of ∠BAC . If AB=10 cm , AC = 14 cm and BC = 6 cm , then find BD and DC .
 A2.5 cm , 3.5 cmB3 cm , 3 cmC3.5 cm , 4.5 cmD4 cm , 2 cm
A2.5 cm , 3.5 cmB3 cm , 3 cmC3.5 cm , 4.5 cmD4 cm , 2 cmAssertion (A) : AD is angle bisector of ∠A of the triangle ABC. If AB = 6 cm, BC = 7 cm, AC = 8 cm then BD = 3 cm and CD = 4 cm.
Reason (R) : The angle bisector AD of the triangle divides base BC in the ratio AB : AC.ABoth Assertion A and Reason R are correct and Reason R is a correct explanation of Assertion A.BBoth Assertion A and Reason R are correct but Reason R is not the correct explanation of Assertion A.CAssertion A is correct, Reason R is wrong.DAssertion A is wrong, Reason R is correct.In the given figure , Ad is the bisector of ∠BAC. If AB = 10 cm , AC = 14 cm and BC = 8 cm , find BD and DC respectively .
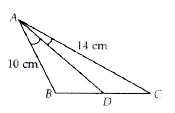 A4.7cm,3.3cmB3.3cm,4.7cmC4.3cm,3,5cmD3.5cm,4.3cm
A4.7cm,3.3cmB3.3cm,4.7cmC4.3cm,3,5cmD3.5cm,4.3cm
In the given figure, AD is the bisector of ∠BAC. If AB =10 cm , AC=6 cm and BC=12 cm, find BD and DC .
View SolutionThe bisector of ∠A in △ABC meets BC in D. If AB = 15 cm, AC = 13 cm and BC = 14 cm, then DC =?
View SolutionIn △ABC, AD is the internal bisector of ∠S, meeting the side BC at D. If BD = 5cm, BC = 7.5 cm, then AB:AC is:
View SolutionIn figure AD is the bisector of ∠BAC. If BD=2cm,CD=3cmandAB=5cm. Find AC :

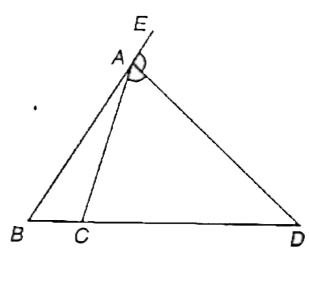
View SolutionIn the figure AD is the external bisector of ∠EAC, intersects BC produced to D. IF AB=12cm,AC=8cmandBC=4cm, find CD :
View Solution
