Question

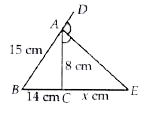
The bisector of $\angle A$ in $△ABC$ meets BC in D. If AB = 15 cm, AC = 13 cm and BC = 14 cm, then DC =?

Options

A. 8.5 cm
B. 8 cm
C. 6.5 cm
D. 7.5 cm

Explanation

To find the length of segment DC in triangle ABC where the angle bisector of angle A meets side BC at point D, we can use the Angle Bisector Theorem.

1. Identify the Given Values:
- AB = 15 cm
- AC = 13 cm
- BC = 14 cm
- Let DC = x cm. Therefore, BD = BC - DC = 14 - x cm.

2. Apply the Angle Bisector Theorem:
According to the Angle Bisector Theorem, we have:
\( \frac{AB}{AC} = \frac{BD}{DC} \)
Substituting the known values:
\( \frac{15}{13} = \frac{14 - x}{x} \)

3. Cross-Multiply to Solve for x:
Cross-multiplying gives us:
\( 15x = 13(14 - x) \)
Expanding the right side:
\( 15x = 182 - 13x \)

4. Combine Like Terms:
Adding 13x to both sides:
\( 15x + 13x = 182 \)
This simplifies to:
\( 28x = 182 \)

5. Solve for x:
Dividing both sides by 28:
\( x = \frac{182}{28} = 6.5 \text{ cm} \)

6. Conclusion:
Therefore, the length of segment DC is:
\( DC = 6.5 \text{ cm} \)