In an equilateral triangle ABC , D is the mid-point of AB and E is the mid-point of AC. Find the ratio between ar (△ABC):ar(△ADE)
Text Solution
The correct Answer is:4:1
|
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Revision Exercise Long Questions
4 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Revision Exercise Very Short Questions
9 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
Knowledge Check
In △ABC, P is the mid-point of BC and Q is the mid-point of AP. Find the ratio of the area of △ABQ and the area of ∠ABC. The following are the steps involved in solving the above problem.
A) We know that a a median of a triangle divides a triangle into two triangles of equal area.
B) ⇒Ar(△ABP)=12[Ar(△ABC)]
C) Ar(△ABQ)=12[Ar(△ABP)]=14[Ar(△ABC)]
D) ⇒(△ABQ):Ar(△ABC)=1:4AABCDBADBCCABCDDADCBIn a triangle ABC, it is known that AB=AC. Suppose D is the mid-point of AC and BD=BC=2. Then the area of the triangle ABC is-
A2B2√2C√7D2√7
In the given figure, D is the mid-point of BC, E is the mid-point of BD and O is the mid-point of AE. Find the ratio of area of ΔBOEandΔABC

View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar(△BED)=14ar(△ABC).
View SolutionInΔABC,AD is the bisector of∠A meeting BC at D, CF⊥AB and E is the mid-point of AC. Then median of the triangle is
View SolutionIn ABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ADE and ABC .
View SolutionIf in a triangle ABC and D, E are the mid-points of AB and AC respectively, then →DE is equal to
View SolutionThe vertex A of △ABC is joined to a point D on the side BC. The midpoint of AD is E.
Prove that ar(△BEC)=12ar(△ABC).
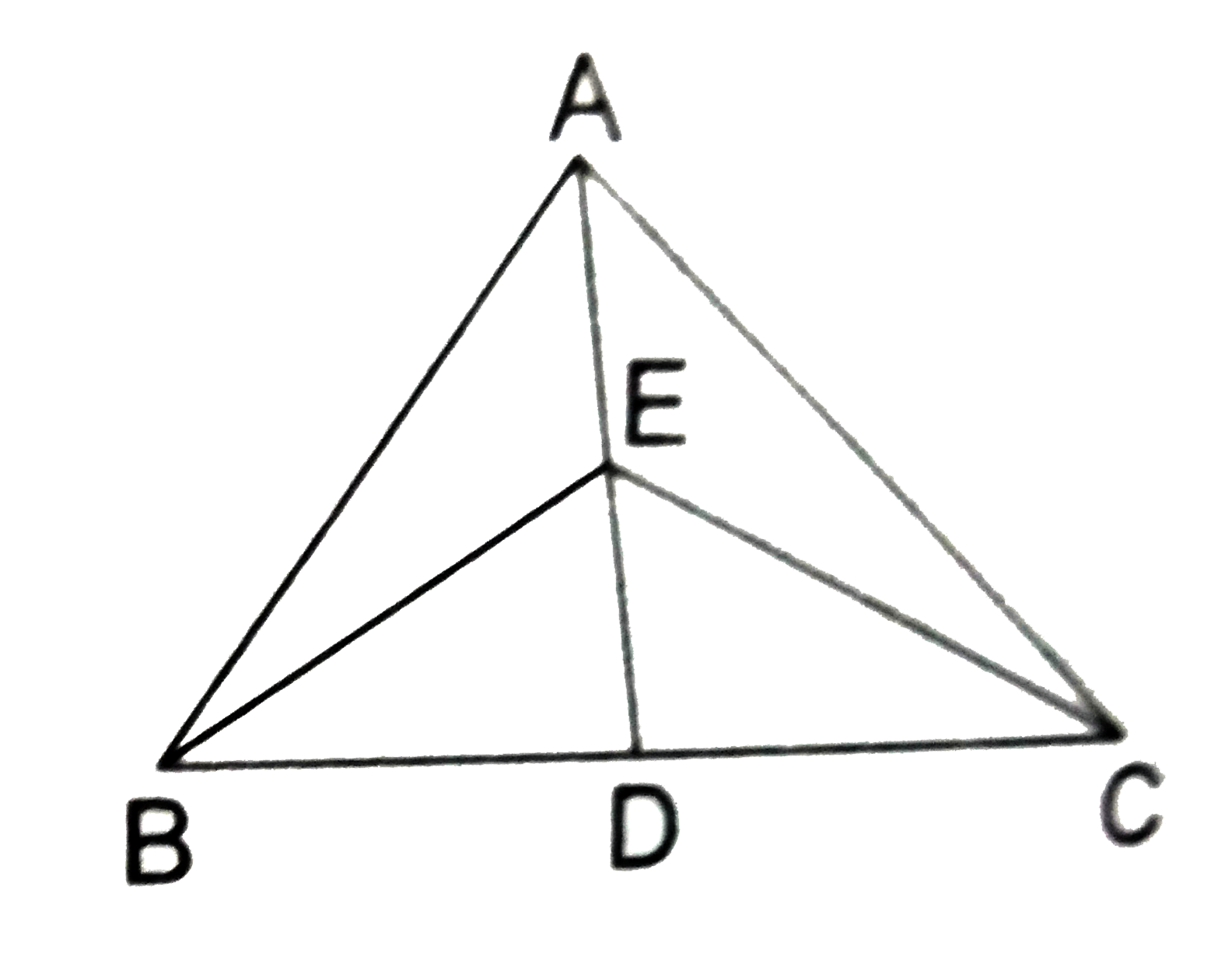
View Solution

