If O, H and G represents circum centre, orthocentre and centroid respectively, then show
HG:GO=2:1. We have,
The correct Answer is:HG:GO=2:1
To show that HG:GO=2:1, where O, H, and G represent the circumcenter, orthocenter, and centroid of a triangle respectively, we can follow these steps:
Step 1: Understand the Definitions
- Circumcenter (O): The point where the perpendicular bisectors of the sides of the triangle intersect.
- Orthocenter (H): The point where the altitudes of the triangle intersect.
- Centroid (G): The point where the medians of the triangle intersect. The centroid divides each median in the ratio 2:1.
Step 2: Draw the Triangle
Let’s consider triangle ABC and plot points O, H, and G on it. Draw the triangle and label the vertices A, B, and C.
Step 3: Draw the Altitude and Median
- Draw the altitude from vertex A to side BC and label the foot of the altitude as point D.
- Draw the median from vertex A to the midpoint E of side BC.
Step 4: Identify the Points
- Mark the orthocenter H at the intersection of the altitudes.
- Mark the centroid G at the intersection of the medians.
- Mark the circumcenter O at the intersection of the perpendicular bisectors.
Step 5: Prove Triangles Congruence
To find the ratio HG:GO, we will show that triangles AHG and EGO are similar:
- Angle HAG is equal to angle EGO: These angles are alternate interior angles.
- Angle AGH is equal to angle GEO: These angles are vertically opposite angles.
By the AA criterion, triangles AHG and EGO are similar.
Step 6: Use the Properties of the Centroid
Since G is the centroid, it divides the median AE into two segments:
- AG=2⋅GE
Step 7: Set Up the Proportions
From the similarity of triangles AHG and EGO:
AGEG=HGGO
Substituting AG=2⋅GE:
2⋅GEGE=HGGO
This simplifies to:
2=HGGO
Step 8: Conclude the Ratio
Thus, we find that:
HG:GO=2:1
- Circumcenter (O): The point where the perpendicular bisectors of the sides of the triangle intersect.
- Orthocenter (H): The point where the altitudes of the triangle intersect.
- Centroid (G): The point where the medians of the triangle intersect. The centroid divides each median in the ratio 2:1.
Let’s consider triangle ABC and plot points O, H, and G on it. Draw the triangle and label the vertices A, B, and C.
- Draw the altitude from vertex A to side BC and label the foot of the altitude as point D.
- Draw the median from vertex A to the midpoint E of side BC.
- Mark the orthocenter H at the intersection of the altitudes.
- Mark the centroid G at the intersection of the medians.
- Mark the circumcenter O at the intersection of the perpendicular bisectors.
To find the ratio HG:GO, we will show that triangles AHG and EGO are similar:
- Angle HAG is equal to angle EGO: These angles are alternate interior angles.
- Angle AGH is equal to angle GEO: These angles are vertically opposite angles.
Since G is the centroid, it divides the median AE into two segments:
- AG=2⋅GE
From the similarity of triangles AHG and EGO:
AGEG=HGGO
Substituting AG=2⋅GE:
2⋅GEGE=HGGO
This simplifies to:
2=HGGO
Thus, we find that:
HG:GO=2:1
Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - SOLVED EXAMPLES
1 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 1
20 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Let O, O' and G be the circumcentre, orthocentre and centroid of a ΔABC and S be any point in the plane of the triangle.
Statement -1: −−−→O'A+−−−→O'B+−−−→O'C=2−−−→O'O
Statement -2: −→SA+−−→SB+−−→SC=3−−→SG
View SolutionThe vertices of a triangle are A(−10,8),B(14,8) and C(−10,26). Let G, I, H, O be the centroid, incentre, orthocentre, circumcentre respectively of ΔABC.
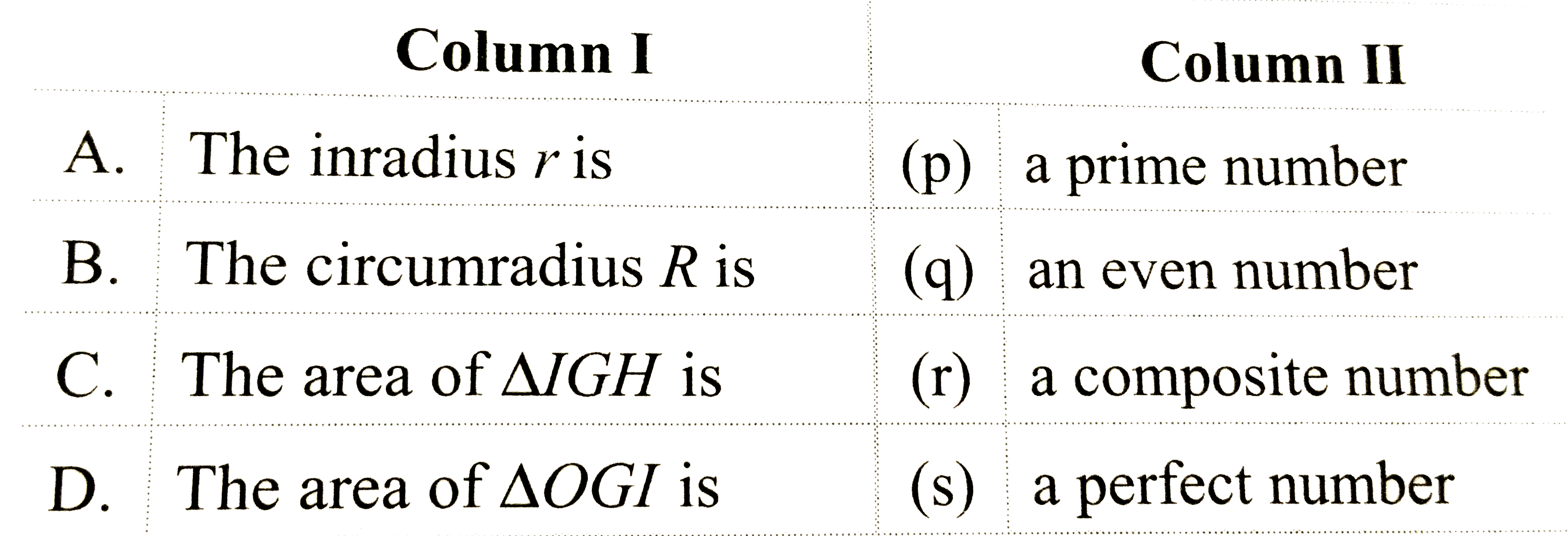
View SolutionABC is a triangle whose circumcentre, incentre and orthocentre are O, I and H respectively which lie inside the triangle, then :
View SolutionIf O is the circumcentre, G is the centroid and O' is orthocentre or triangle ABC then prove that: −−→OA+−−→OB+−−→OC=−−−→OO'
View SolutionStatement 1: If in a triangle, orthocentre, circumcentre and centroid are rational points, then its vertices must also be rational points.
Statement : 2 If the vertices of a triangle are rational points, then the centroid, circumcentre and orthocentre are also rational points.
View SolutionIf the coordinates of orthocentre O' are centroid G of a ΔABC are (0,1) and (2,3) respectively, then the coordinates of the circumcentre are
View SolutionStatement 1 : If the vertices of a triangle are having rational coordinates, then its centroid, circumcenter, and orthocentre are rational. Statement 2 : In any triangle, orthocentre, centroid,and circumcenter are collinear, and the centroid divides the line joining the orthocentre and circumcenter in the ratio 2:1.
View SolutionIf the orthocentre and centroid of a triangle are (-3, 5, 1) and (3, 3, -1) respectively, then its circumcentre is
View SolutionLet the orthocentre and centroid of a triangle be A(−3,5)andB(3,3) respectively. If C is the circumcentre of the triangle then the radius of the circle having line segment AC as diameter, is
View SolutionIf S is the cirucmcentre, G the centroid, O the orthocentre of a triangle ABC, then −→SA+−−→SB+−−→SC is:
View Solution
