If O is the circumcentre of a ABC and OD⊥BC, prove that ∠BOD=∠a.
Given In a ΔABC a circle is circumscribed having centreO.
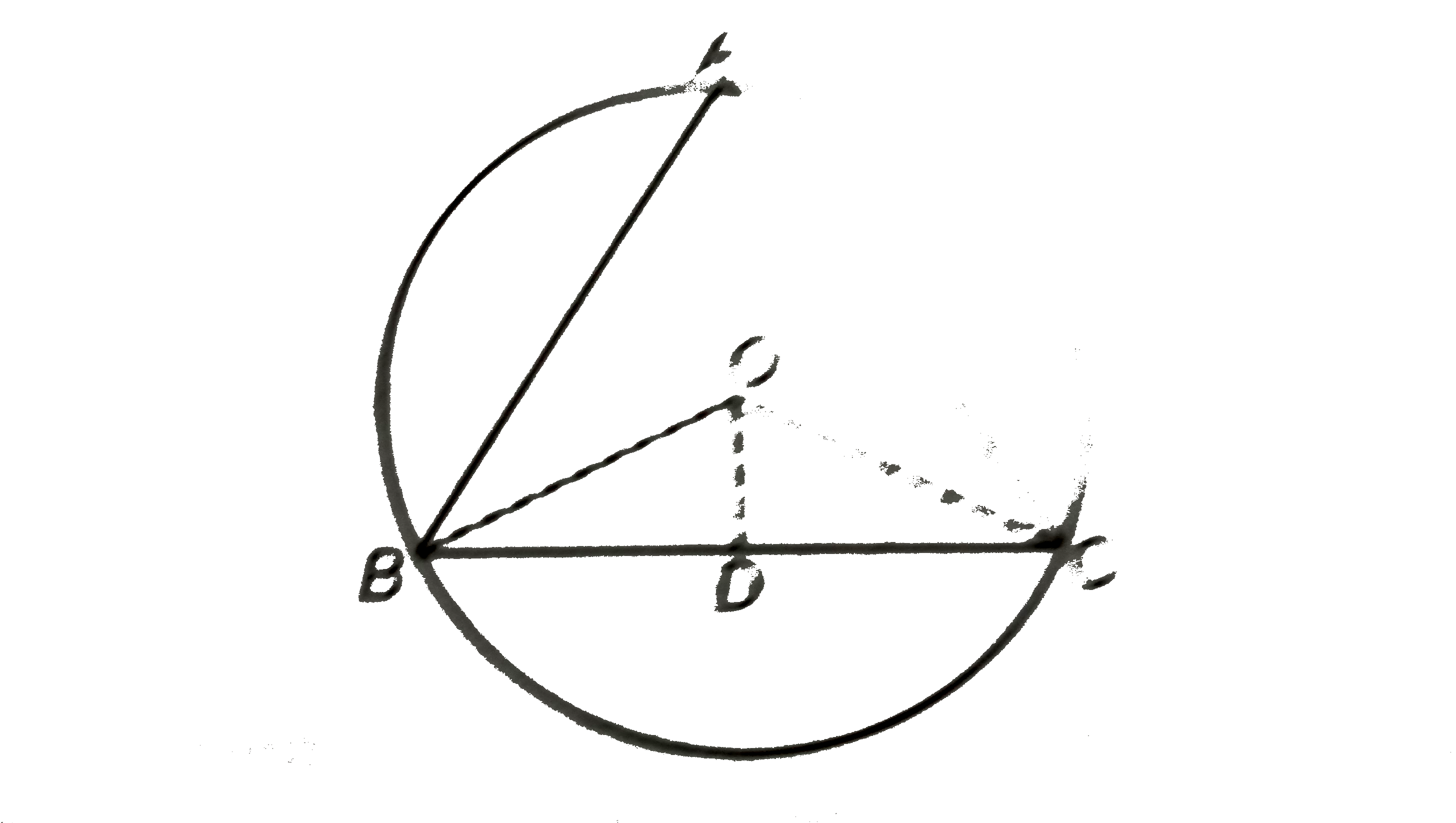
Also, D is the mid-point of BC.
To prove ∠BOD=∠Aor∠BOD=∠BAC
Construction Join OB, OD and OC.
Proof In ΔBODandΔCOD,
OB=OC [both are the radius of circle]
BD=DC [D is the mid-point of BC]
and OD=OD [common side]
∴ΔBOD≅ΔCOD [by SSS congruence rule]
∴∠BOD=∠COD [by CPCT]...(i)
We know that, in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.
∴2∠BAC=∠BOC
⇒∠BAC=22∠BOD[∵∠BOC=2∠BOD] [from Eq. (i)]
⇒∠BAC=∠BOD
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
If 'O' is the circum centre of the ABC and R1, R2, R3 are the radii of the circumcircle of triangle OBC, OCA and OAB respectively then aR1+bR2+cR3 has the value equal to abc2R3 (b) R3abc (c) 4R2 (d) abcR3
View SolutionBisector AD of ∠BAC of ABC passes through the centre O of the circumcircle of ABC as shown in figure. Prove that AB=AC.
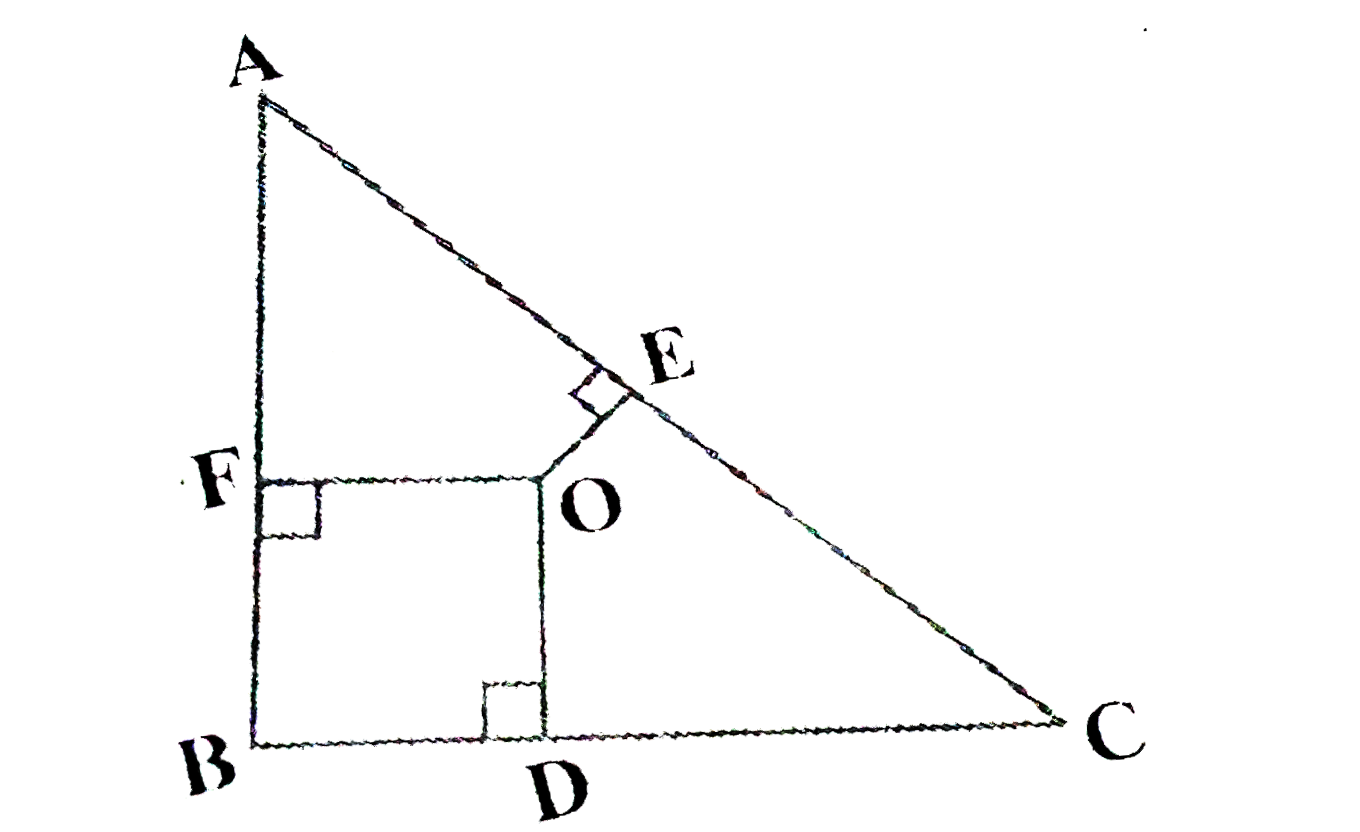
View SolutionIn figure, O is a point in the interior of a triangle ABC, OD⊥BC,OE⊥ACand OF⊥AB. Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AW2+CD2+BF2
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(BOE)=18ar(ABC)
View SolutionIf a<b and c≤d, prove that a+c<b+d
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE, prove that ar ( BOE)=18ar ( ABC)
View SolutionIf O and O′ are circumcentre and orthocentre of ABC, then →OA+→OB+→OC equals
a.2→OO' b. →OO' c. →O'O d. 2→O'O
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(AOD)=ar(BOC) . Prove that ABCD is a trapezium.
View SolutionIn figure, ABC is triangle in which ∠ABC=90∘and AD⊥CBproduced. Prove that AC2=AB2+BC2−2BC.BD.

View SolutionABCD is a parallelogram whose diagonals AC and BD intersect at O. A Line through O intersects AB at P and DC at Q. Prove that ar(△POA)=ar(△QOC).
View Solution
