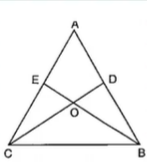
Bisector AD of ∠BAC of ABC passes through the centre O of the circumcircle of ABC as shown in figure. Prove that AB=AC.
Given: Bisector AD of ∠BAC of △ABC passed through the centre O of the circumcircle of △ABC
To Prove: AB=AC
Construction: Draw OP⊥AB and OQ⊥AC
Proof: In △APO and △AQO,
∠OPA=∠OQA [Each=90∘ (By construction)]
∠OAP=∠OAQ [Given]
OA=OA [Common]
∴△APO≅△AQO [By SAS]
∴OP=OQ [By CPCT]
∴AB=AC [since, Chords equidistant from the centre are equal]
Hence, AB=AC
Topper's Solved these Questions
Similar Questions
In Figure., ABC is a triangle in which ∠BAC=300. Show that BC is the radius of the circumcircle of ABC, whose centre is O.

View SolutionA point D is taken on the side BC of a ABC such that BD=2dC. Prove that ar(ABD)=2ar(ADC).
View SolutionABCD is such a quadrilateral that A is the centre of the circle passing through B,CandD. Prove that ∠CBD+∠CDB=12∠BAD.
View SolutionBisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90∘−12A,90∘−12Band 90∘−12C
View SolutionABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P as shown in Figure. Prove that ar (ABP)=ar (Qua..ABCD).
View SolutionIn Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD

View SolutionO is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(OAB)=ar(OBC)
View SolutionBM and CN are perpendicular to a line passing through the vertex A of a triangle ABC. If L is the mid-point of BC , prove that LM=LN
View SolutionA circle passes through A,B,C and D as shown in the figure. If ∠BAD=63∘, find x.
View SolutionIn Figure, it is given that AE=AD and BD=CE. Prove that AEB≅ADC
View Solution