If R is any point on the x-axis and Q is any point on they y-axis and P is a variable point on RQ with RP=b, PQ=a, then find the equation of locus of P.Solution in Tamil
x+y=1
x+y=2
x+y=2xy
2x+2y=1
The correct Answer is:A
The equation of line AB is y-1 = m(x-1). Therefore, the equation of line AC is
y−1=−1m(x−1)
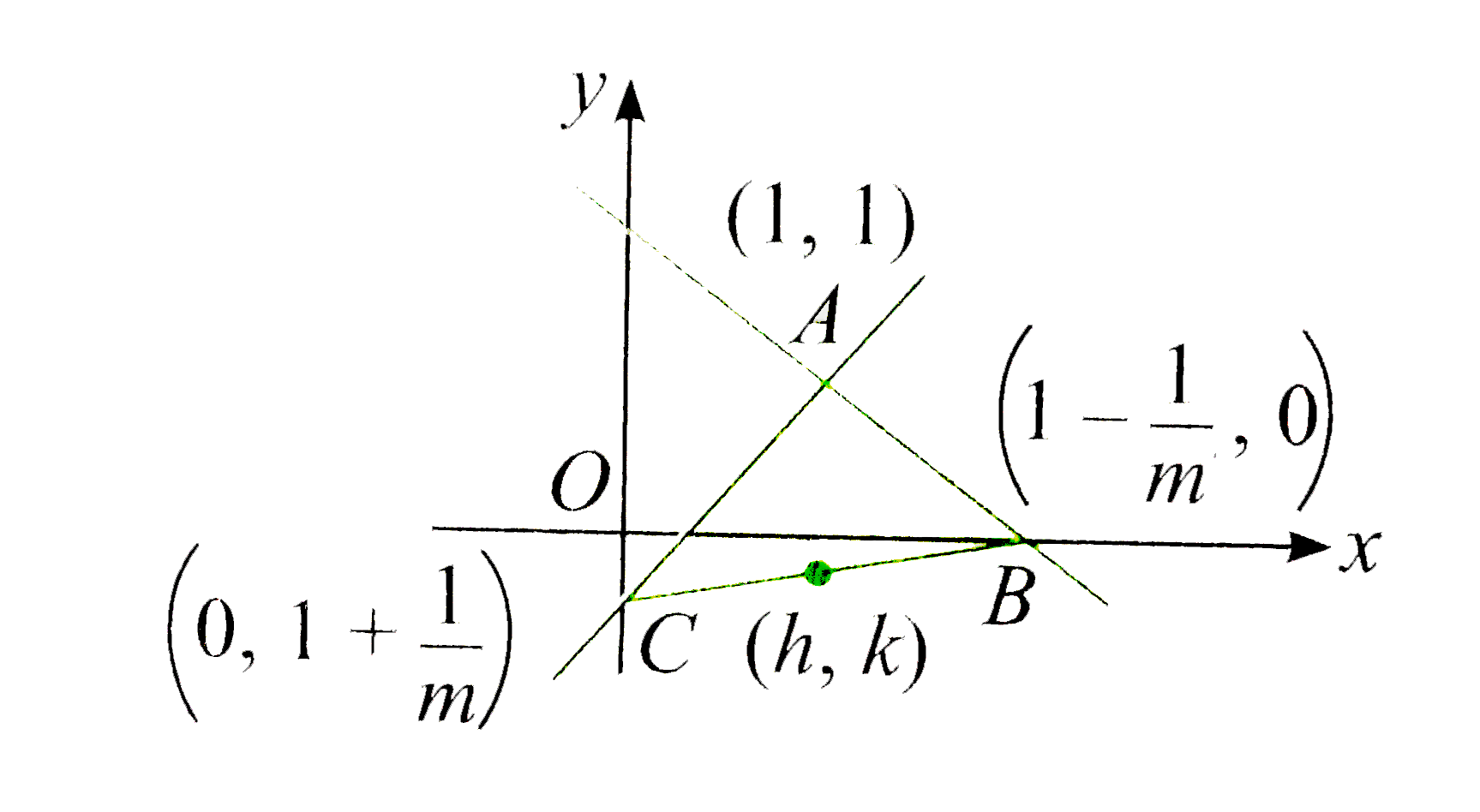
2h=1−1m
2k=1+1m
Eliminating m, we have locus x+y=1.
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Multiple)
30 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)
27 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.6
5 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
View SolutionLet L be the line belonging to the family of straight lines (a+2b) x+(a-3b)y+a-8b =0, a, b ∈R, which is the farthest from the point (2, 2).
Area enclosed by the line L and the coordinate axes is
View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
View SolutionA is any point on X -axis and B is any point of Y- axis and P is a variable point on AB with PA=b and PB=a and AB=a+b. Find the equation of locus of P
View SolutionA line intersects the y-axis and x-axis at the points P and Q respectively. If (2, 5) is the mid-point of PQ, then find the coordinates of P and Q.
View SolutionThe tangent at any point P on y^(2)=4x meets x-axis at Q, then locus of mid point of PQ will be
View SolutionA line intersect the Y-axis and X-axis at he points P and Q respectively. If (2,-5) is the mid-point of PQ, then find the coordinate of P and Q.
View Solutionएक रेखा Y-अक्ष और X-अक्ष को क्रमश: बिन्दुओ P और Q पर काटती है । यदि PQ का मध्य-बिंदु (2, -5) है, तो P और Q के निर्देशांक ज्ञात कीजिए ।
View SolutionLet P be (5,3) and a point R on y = x and Q on the X - axis be such that PQ+QR+RP is minimum ,then the coordinates of Q are
View SolutionIf R is any point on the x-axis and Q is any point on they y-axis and P is a variable point on RQ with RP=b, PQ=a, then find the equation of locus of P.
View Solutionएक रेखा x-अक्ष को A(7, 0) पर तथा y-अक्ष को B(0, -5) पर काटती है। के AB लंबवत एक चर रेखा PQ खींची जाती है जो x-अक्ष को बिंदु P पर तथा y-अक्ष को बिंदु Q पर काटती है। यदि AQ और BP, बिंदु R पर प्रतिच्छेद करती है , तो R का बिन्दुपथ होगा
View SolutionR மற்றும் Q என்பன முறையே x மற்றும் y அச்சுகளின் மீது அமைந்துள்ள புள்ளிகள், P என்ற நகரும் புள்ளி RQ-ன் மேல் உள்ளது. மேலும் RP = b, PQ = a என்றவாறு RQ-ன் மீது அமைந்துள்ள நகரும் P-ன் நியமப்பாதையின் சமன்பாட்டைக் காண்க.
View SolutionA line intersects the y-axis and x-axis at the points P and Q respectively. If (2,-5) is the mid-point of PQ then find the coordinates of P and Q.
View SolutionA line intersects y-axis and x-axis at the points P and Q respectively. If (2, 5) is the mid point of PQ then find the co ordinates of P and Q.
View Solution
