If of students scored less than 33 marks, then find r, given , class size=, frequency of the rth. Percentile class and cumulative frequency of the rth percentile class , lower limit of rth percentile class
The correct Answer is:
To solve the problem step by step, we will use the given data and apply the formula for calculating percentiles.
Given Data:
- Total number of students, N=50
- Class size, H=10
- Frequency of the rth percentile class, f=12
- Cumulative frequency of the rth percentile class, CF=22
- Lower limit of the rth percentile class, L=30
- Minimum marks to be considered, X=33
Step 1: Write the formula for the rth percentile
The formula for the rth percentile is given by:
X=L+N⋅(r100)−CFf⋅H
Step 2: Substitute the known values into the formula
Substituting the known values into the formula:
33=30+50⋅(r100)−2212⋅10
Step 3: Simplify the equation
First, subtract 30 from both sides:
33−30=50⋅(r100)−2212⋅10
This simplifies to:
3=50⋅(r100)−2212⋅10
Step 4: Multiply both sides by 12 to eliminate the denominator
3⋅12=(50⋅(r100)−22)⋅10
This gives:
36=(50⋅(r100)−22)⋅10
Step 5: Divide both sides by 10
3610=50⋅(r100)−22
This simplifies to:
3.6=50⋅(r100)−22
Step 6: Add 22 to both sides
3.6+22=50⋅(r100)
This gives:
25.6=50⋅(r100)
Step 7: Multiply both sides by 10050
25.6⋅10050=r
This simplifies to:
r=51.2
Conclusion
Thus, the value of r is 51.2.
---
- Total number of students, N=50
- Class size, H=10
- Frequency of the rth percentile class, f=12
- Cumulative frequency of the rth percentile class, CF=22
- Lower limit of the rth percentile class, L=30
- Minimum marks to be considered, X=33
The formula for the rth percentile is given by:
Substituting the known values into the formula:
First, subtract 30 from both sides:
3⋅12=(50⋅(r100)−22)⋅10
3610=50⋅(r100)−22
3.6+22=50⋅(r100)
25.6⋅10050=r
Thus, the value of r is 51.2.
Topper's Solved these Questions
Similar Questions
From a frequency distribution, c = 3, l = 65 . 5 f = 42, m = 23, N = 102 then median is (l = lower limit of the median class, m= cumulative frequency of the class preceeding the median class, N = total frequency, f = frequency of the median class, c = width of the median class)
View SolutionIn a frequency distribution, the mid values of a class is 10 and width of the class is 6. The lower limit of the class is
View SolutionWhile calculating mode the following observation are found. Lower limit of modal class =40, frequency of modal class =20, frequency of previous class =12 , frequency of preceding class =11 and width of the class =10, find mode .
View SolutionIn a frequency distribution, the mid-value of a class is 15 and the class intervals is 4. The lower limit of the class is 10 (b) 12 (c) 13 (d) 14
View SolutionThe width of each of five continuous classes in a frequency distribution is 5 and the lower class limit of the lowest class is 10. The upper class limit of the highest class is
View SolutionTally marks are used to find
(a) class interval (b) range
(c) frequency (d) upper limit
View SolutionConsider the marks obtained (out of 100 marks) by 30 students of Class IX of a school: 10 20 36 92 95 40 50 56 60 7092 88 80 70 72 70 36 40 36 4092 40 50 50 56 60 70 60 60 88 Recall that the number of students who have obtained a certain number of marks is called the frequency of those marks. For instance, 4 students got 70 marks. So the frequency of 70 marks is 4. To make the data more easily understandable, tabulate the data.
View SolutionThe table , given below , shows the frequency distributions of the weekly wages of the employee of a company:
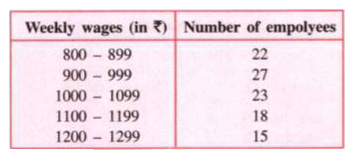
Find :
(i) the lower limit of the fourth class.
(ii) the upper limit of the fifth class.
(iii) the class boundaries of the second class.
(iv) the class mark of the first class.
(v) the class size of the third class.
(vi) cumulative frequency of the fourth class.
View SolutionGiven below is a cumulative frequency distribution showing the mars secured by 50 students of a class

From the frequency distribution table for the data.
View SolutionFind the class limits corresponding to each frequency if the mean of the following distribution is 33 and assumed mean 35 :

View Solution
