If $sec θ = \frac{5}{4}, find the value of \frac{(2 cos θ - sin θ)}{(cot θ - tan θ)} = .$

A

(12)/(7)

B

(12)/(5)

C

(1)/(7)

D

(2)/(5)

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

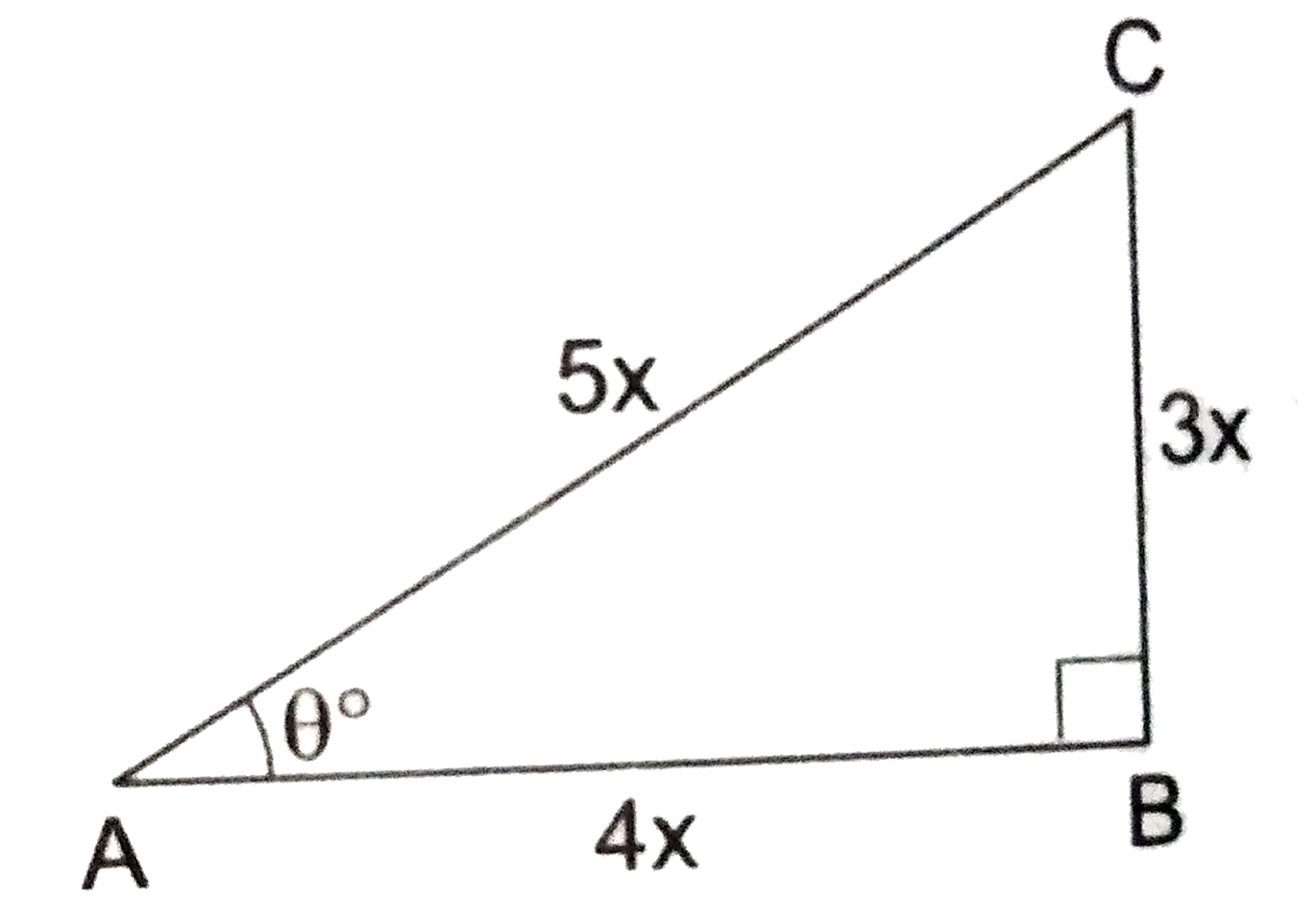
Consider a $Δ A B C in which ∠ A = θ and ∠ B = 90^{\circ}$ .
$sec θ = \frac{hypotenuse}{base} = \frac{A C}{A B} = \frac{5}{4} = \frac{5 x}{4 x} (say)$
$∴ A C = 5 x and A B = 4 x, where x$ is positive .
By pythagoras' theorem we have
$A C^{2} = A B^{2} + B C^{2}$
$\Rightarrow B C^{2} = A C^{2} - A B^{2} = {(5 x)}^{2} - {(4 x)}^{2} = 9 x^{2}$
$\Rightarrow B C = 3 x .$
$∴ cos θ = \frac{A B}{A C} = \frac{4 x}{5 x} = \frac{4}{5}, sin θ = \frac{B C}{A C} = \frac{3 x}{5 x} = \frac{3}{5},$
$cot θ = \frac{A B}{B C} = \frac{4 x}{3 x} = \frac{4}{3}, and tan θ = \frac{B C}{A B} = \frac{3 x}{4 x} = \frac{3}{4} .$
$∴ \frac{(2 cos θ - sin θ)}{(cot θ - tan θ)} = \frac{(2 \times \frac{4}{5} - \frac{3}{5})}{(\frac{4}{3} - \frac{3}{4})} = \frac{(\frac{8}{5} - \frac{3}{5})}{(\frac{4}{3} - \frac{3}{4})} = \frac{(\frac{5}{5})}{(\frac{7}{12})} = \frac{1}{(\frac{7}{12})} = \frac{12}{7} .$

|

Class 10 MATHS TRIGONOMETRIC RATIOS AND IDENTITIES

Topper's Solved these Questions

Similar Questions

Knowledge Check

If $cos θ = \frac{3}{5}, find the value of (\frac{5 cosec θ - 4 tan θ}{sec θ + cot θ}) .$
A $\frac{24}{29}$
B $\frac{1}{29}$
C $\frac{8}{29}$
D $\frac{11}{29}$
If $sin θ = 5 / 13$ , then find the value of (cot $θ - tan θ) / 2 cot θ$ ?
A143/195
B119/254
C173/288
D119/288
If $cos e c θ = \sqrt{5} / 2$ , find the value of $sec θ + tan θ - cot θ$ .
A $(3 + 2 \sqrt{5}) / 2$
B $(3 - 2 \sqrt{5}) / 2$
C $(2 - 2 \sqrt{5}) / 2$
D $(2 + 2 \sqrt{5}) / 2$

RS AGGARWAL-TRIGONOMETRIC RATIOS-Exercise 10

Home
Ask Doubt
Profile