If tanA=√3, find other trigonometric ratios of sinA.
A
2√3
B
√52
C
2
D
√32
Video Solution
Text Solution
The correct Answer is:D
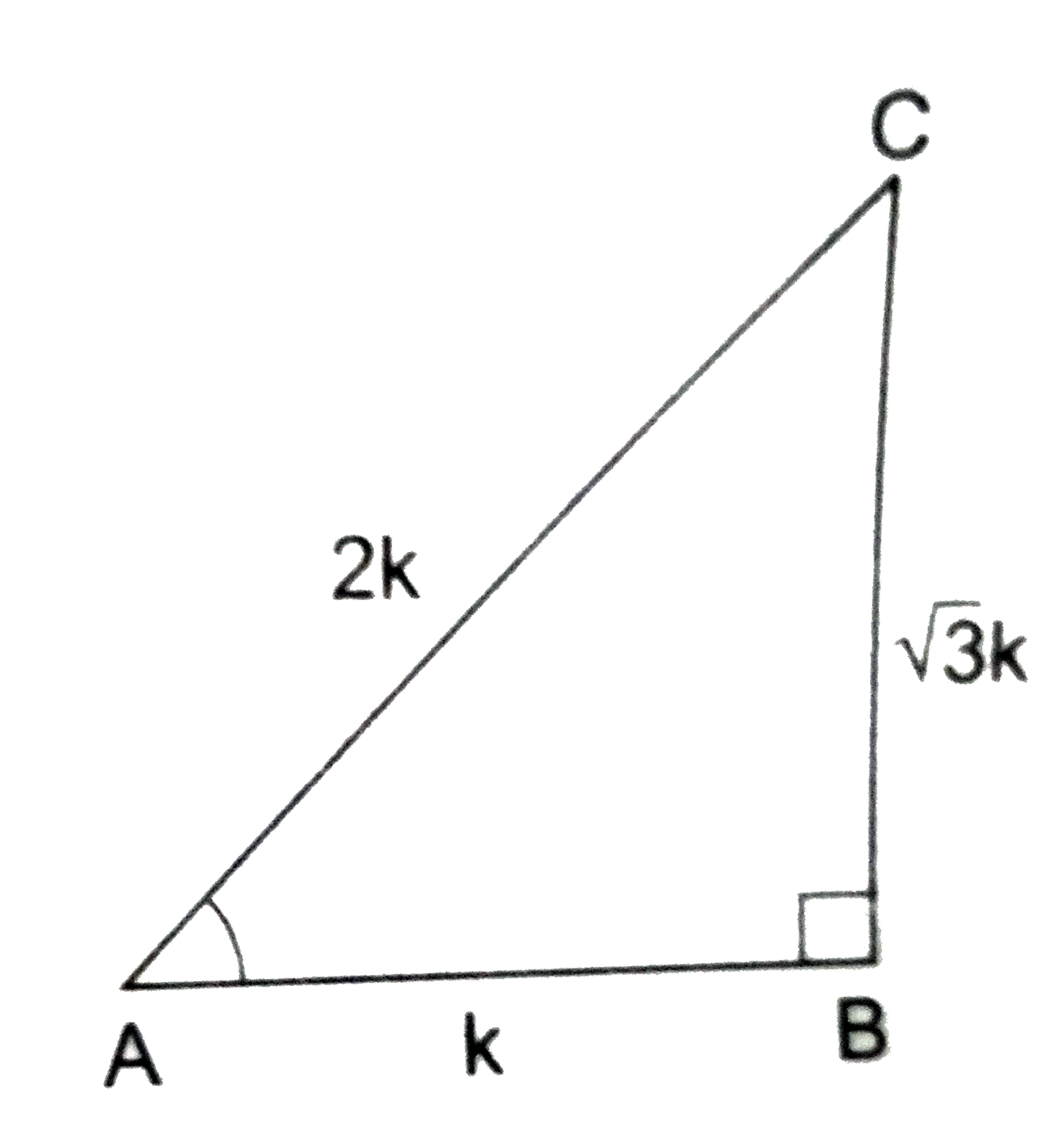
Let us draw aΔABC in which ∠B=90∘.
then ,tanA=BCAB=√31.
Let BC=√3kandAB=k, where k is positive .
by pythagoras' theorem , we have
AC2=AB2+BC2=k2+(√3k)2
=k2+3k2=4k2.
∴AC=√4k2=2k.
∴sinA=BCAC=√3k2k=√32,
cosA=ABAC=k2k=12,
tanA=√3(given),cosecA=1sinA=2√3,
secA=1cosA=2andcotA=1tanA=1√3.
|
Topper's Solved these Questions
- TRIGONOMETRIC RATIOSBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOSEXERCISE - Exercise 10
35 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
- TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES EXERCISE - Exercise 12
15 Videos
Similar Questions
If sinA=23 , find other trigonometric ratios.
View SolutionIf cosecA=√10, find other five trigonometric ratios.
View Solutionsinθ=√32 , find other trigonometric ratios
View SolutionGiven tanA=43, find the other trigonometric ratios of the angle A.
View SolutionIf cosA=45 , find other trigonometric ratios.
View SolutionIf secθ=135 , find other trigonometric ratios
View SolutionIf sinA=817, find other trigonometric ratios of ∠A.
View SolutionIf cosA=941, find other trigonometric ratios of ∠A.
View SolutionIf cosθ=725 , find other trigonometric ratios
View SolutionIf cotθ=125 , find other trigonometric ratios
View Solution
