If the angles of elevation of a tower from two points distant a and b (a>b) from its foot and in the same straight line with it are 30o and 60o , then the height of the tower is √a+b (b) √ab (c) √a−b (d) √ab
Step by step video & image solution for If the angles of elevation of a tower from two points distant a and b (a > b) from its foot and in the same straight line with it are 30o and 60o , then the height of the tower is sqrt(a+b) (b) sqrt(a b) (c) sqrt(a-b) (d) sqrt(a/b) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If the angles of elevation of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is ab (b) √ab (c) ab (d) √ab
View SolutionThe angles of elevation of the top of a tower from two points at distances a and b metres from the base and in the same straight line with it are complementary. Prove that the height of the tower is √ab metres.
View Solution
Knowledge Check
If the angle of elevation of a tower from two distant points a and b (a > b) from its foot and in the same straight line and on the same side of it are 30∘and60∘, then the height of the tower is
Aa )√abBb)√a+bCc) √abDd ) √a−bIf the angles of elevation of the top of a tower from two points at distances a and b from the base and in the same straight line with it are complementary then the height of the tower is
A√abB√abC√a+bD√a−bThe angle of elevation of the top of a tower from the point P and Q at distance of a and b respectively from the base of the tower and in the same straight line with it are complementary .The height of the tower is
A√abBabCabDa2b2
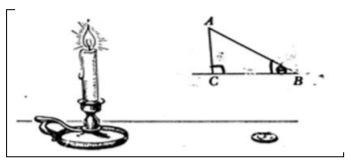
If the angles of elevation of the top of the candle from two coins distant ‘a’ cm and ‘b’ cm (a>b) from its base and in the same straight line from it are 30∘ and 60∘, then find the height of the candle.
View SolutionThe angle of elevation of the top of a tower from two points on the ground at distances a metres and b metres from the base of the tower and in the same straight line are complementary.Prove that height of the tower is√ab.
View SolutionThe angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is √st.
View SolutionThe angle of elevation of the top of a tower from a point 40 m away from its foot is 60∘. Find the height of the tower.
View SolutionThe angles of elevation of the top of a tower at two points, which are at distances a and b from the foot in the same horizontal line and on the same side of the tower, are complementary. The height of the tower is
View Solution
