If the bisectors of a pair of alternate angles formed by a transversal with two given lines are parallel, prove that the given lines are parallel.
To prove that if the bisectors of a pair of alternate angles formed by a transversal with two given lines are parallel, then the given lines are parallel, we can follow these steps:
1. Draw the Figure:
- Let lines AB and CD be two given lines.
- Let a transversal GH intersect these lines at points A and D, forming alternate angles ∠AGH and ∠GHD.
2. Identify the Angles:
- Let the bisector of ∠AGH be line GM and the bisector of ∠GHD be line HL.
- By the property of angle bisectors, we have:
- ∠AGM = ∠1 (half of ∠AGH)
- ∠DHL = ∠2 (half of ∠GHD)
3. Given Condition:
- It is given that GM || HL (the bisectors are parallel).
4. Use the Alternate Angles Property:
- Since GM and HL are parallel and GH is a transversal, we can use the property of alternate interior angles:
- ∠1 = ∠2 (alternate interior angles are equal).
5. Relate the Angles:
- From the angle bisector property, we know:
- ∠AGH = 2∠1 (since GM is the bisector)
- ∠GHD = 2∠2 (since HL is the bisector)
6. Set Up the Equations:
- Since ∠1 = ∠2, we can substitute:
- ∠AGH = 2∠1
- ∠GHD = 2∠1
- Therefore, ∠AGH = ∠GHD.
7. Conclude the Proof:
- Since ∠AGH and ∠GHD are alternate angles formed by the transversal GH, and they are equal, by the Alternate Interior Angles Theorem, we conclude that lines AB and CD are parallel.
Final Statement:
Thus, we have proved that if the bisectors of a pair of alternate angles formed by a transversal with two given lines are parallel, then the given lines are also parallel.
---
- Let lines AB and CD be two given lines.
- Let a transversal GH intersect these lines at points A and D, forming alternate angles ∠AGH and ∠GHD.
- Let the bisector of ∠AGH be line GM and the bisector of ∠GHD be line HL.
- By the property of angle bisectors, we have:
- ∠AGM = ∠1 (half of ∠AGH)
- ∠DHL = ∠2 (half of ∠GHD)
- It is given that GM || HL (the bisectors are parallel).
- Since GM and HL are parallel and GH is a transversal, we can use the property of alternate interior angles:
- ∠1 = ∠2 (alternate interior angles are equal).
- From the angle bisector property, we know:
- ∠AGH = 2∠1 (since GM is the bisector)
- ∠GHD = 2∠2 (since HL is the bisector)
- Since ∠1 = ∠2, we can substitute:
- ∠AGH = 2∠1
- ∠GHD = 2∠1
- Therefore, ∠AGH = ∠GHD.
- Since ∠AGH and ∠GHD are alternate angles formed by the transversal GH, and they are equal, by the Alternate Interior Angles Theorem, we conclude that lines AB and CD are parallel.
Thus, we have proved that if the bisectors of a pair of alternate angles formed by a transversal with two given lines are parallel, then the given lines are also parallel.
Topper's Solved these Questions
Similar Questions
If the bisectors of a pair of corresponding angles formed by a transversal with two given lines are parallel;prove that the given lines are parallel.
View SolutionIf the bisectors of a pair of corresponding angles formed by a transversal with two given lines lines are parallel, prove that the given lines are parallel.
View SolutionWrite converse of the following statement: If a pair of the interior angles made by a transversal of two lines are supplementary then the lines are parallel.
View SolutionTransversal to two parallel lines:
View Solutionprove that two lines m and n be parallel to the same given line are parallel to each other.
View SolutionWrite the converse of, "if the corresponding angles formed by a transversal of two lines are congruent, then two lines are parallel."
View SolutionDraw a line parallel to a given line.
View SolutionAP and BQ are the bisectors of the two alternate interior angles formed by the intersection of a transversal t with parallel lines l and m (in the given figure). Show that AP||BQ.
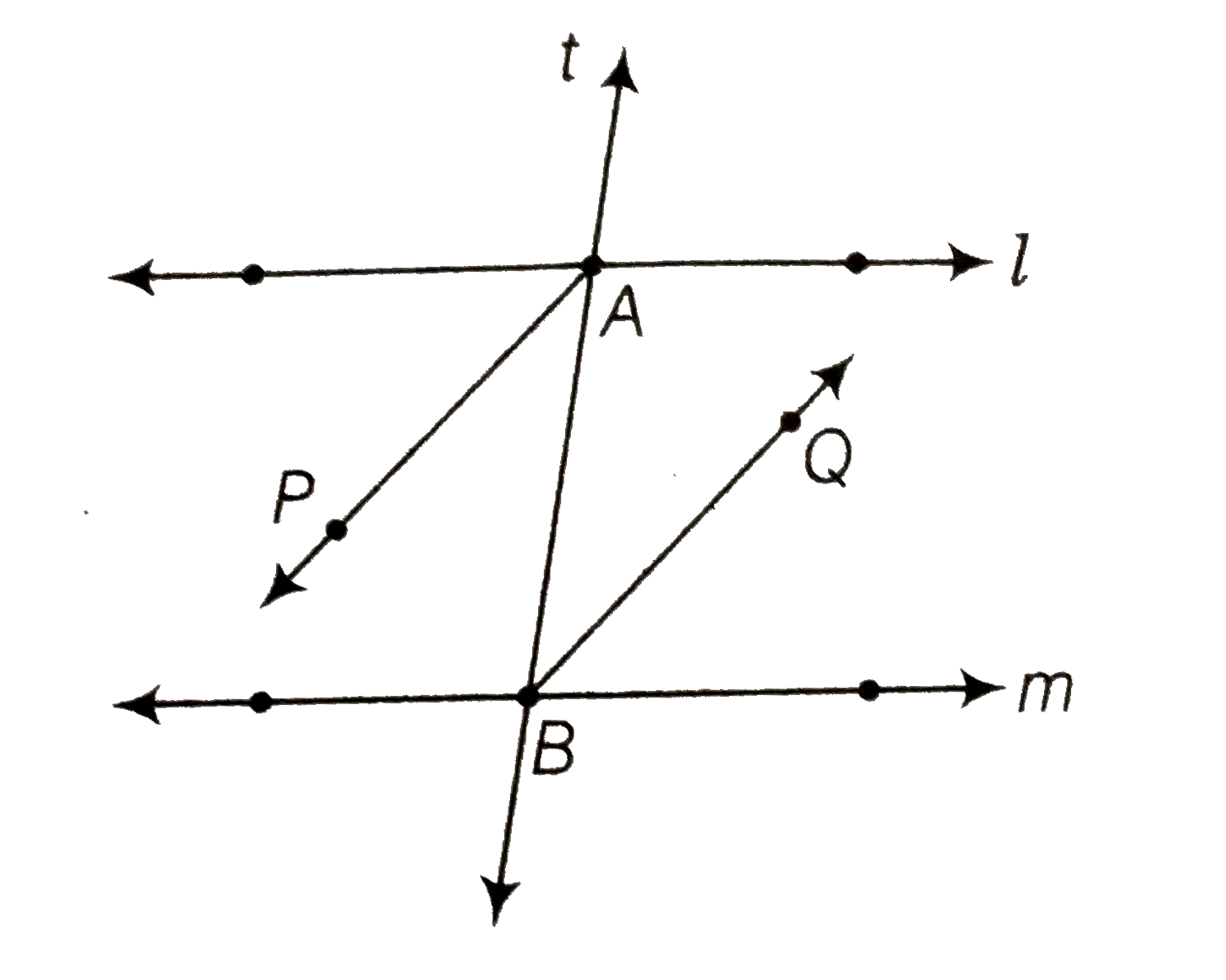
View SolutionParallel Lines and a Transversal
View SolutionIf a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel.
View Solution
