AP and BQ are the bisectors of the two alternate interior angles formed by the intersection of a transversal t with parallel lines l and m (in the given figure). Show that AP||BQ.
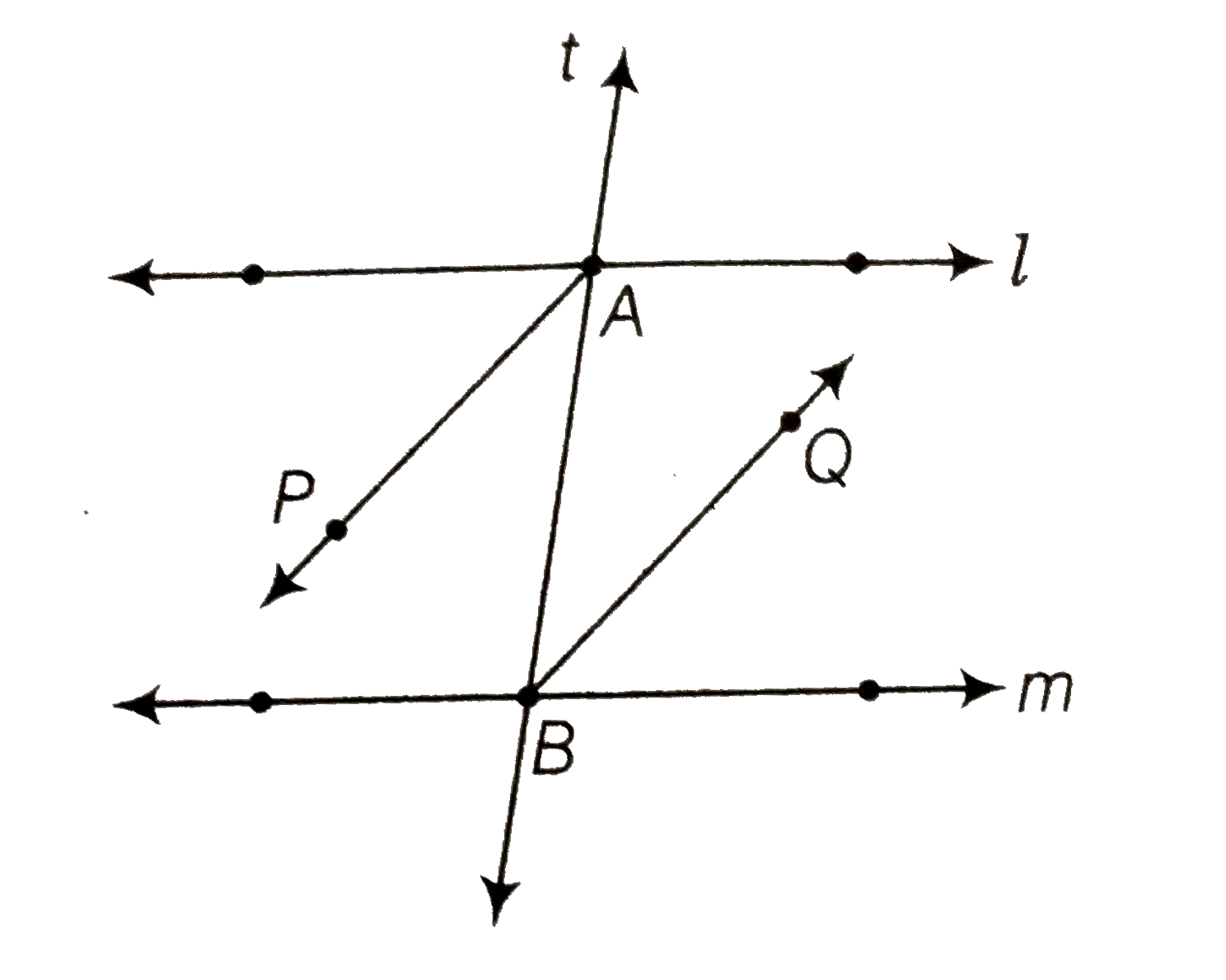
Given In the figure l||m , AP and BQ are the bisectors of ∠EAB and ∠ABH, respectively.
To Prove AP|| BQ
Proof Since, l||m and t is transversal.
Therefore, ∠EAB=∠ABH [alternate interior angles]
⇒ 12∠EAB=12∠ABH [dividing both sides by 2]
⇒ ∠PAB=∠ABQ [AP and BQ are the bisectors of ∠EABand∠ABH]
Since, ∠PAB and ∠ABQ are alternate interior angles with two lines AP and BQ and transversal AB, Hence, AP || BQ.
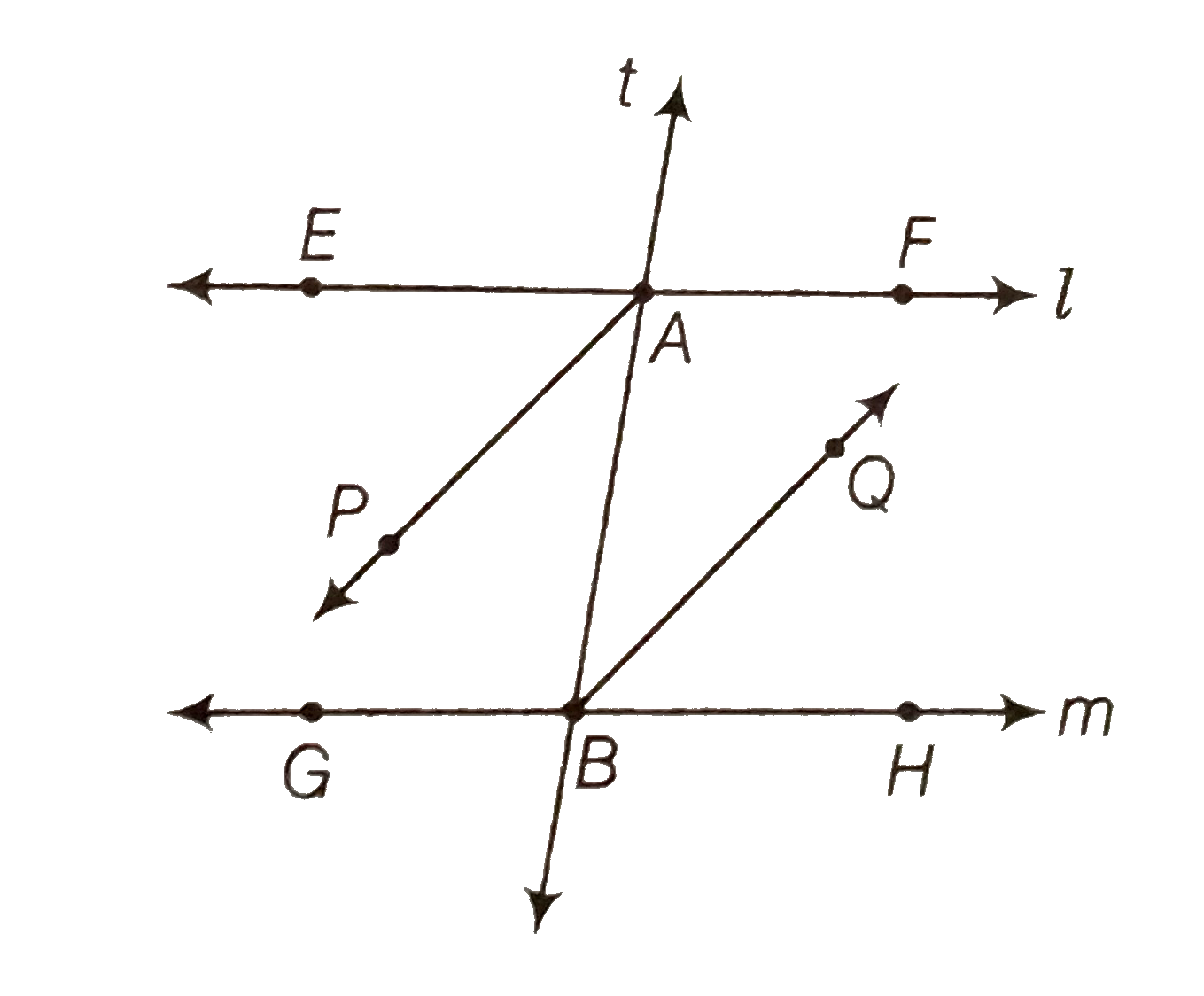
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If two interior angles on the same side of a transversal intersecting two parallel lines are in the ratio 3:2, then the greater of the two angles is :
A72∘B36∘C108∘D44∘ - Question 2 - Select One
If a transversal line cuts two parallel lines then bisector of internal angle formed a
ArectangleBsquareCrhombusDparallelogram
State whether the statements are True or False.
Sum of interior angles on the same side of a transversal with two parallel lines is 90∘View SolutionIf the bisectors of a pair of alternate angles formed by a transversal with two given lines are parallel, prove that the given lines are parallel.
View SolutionState whether the statements are True or False.
Interior angles on the same side of a transversal with two distinct parallel lines are complementary angles.View SolutionIn the given figure, bisectors AP and BQ of the alternate interior angles are parallel, then show that l ||m.
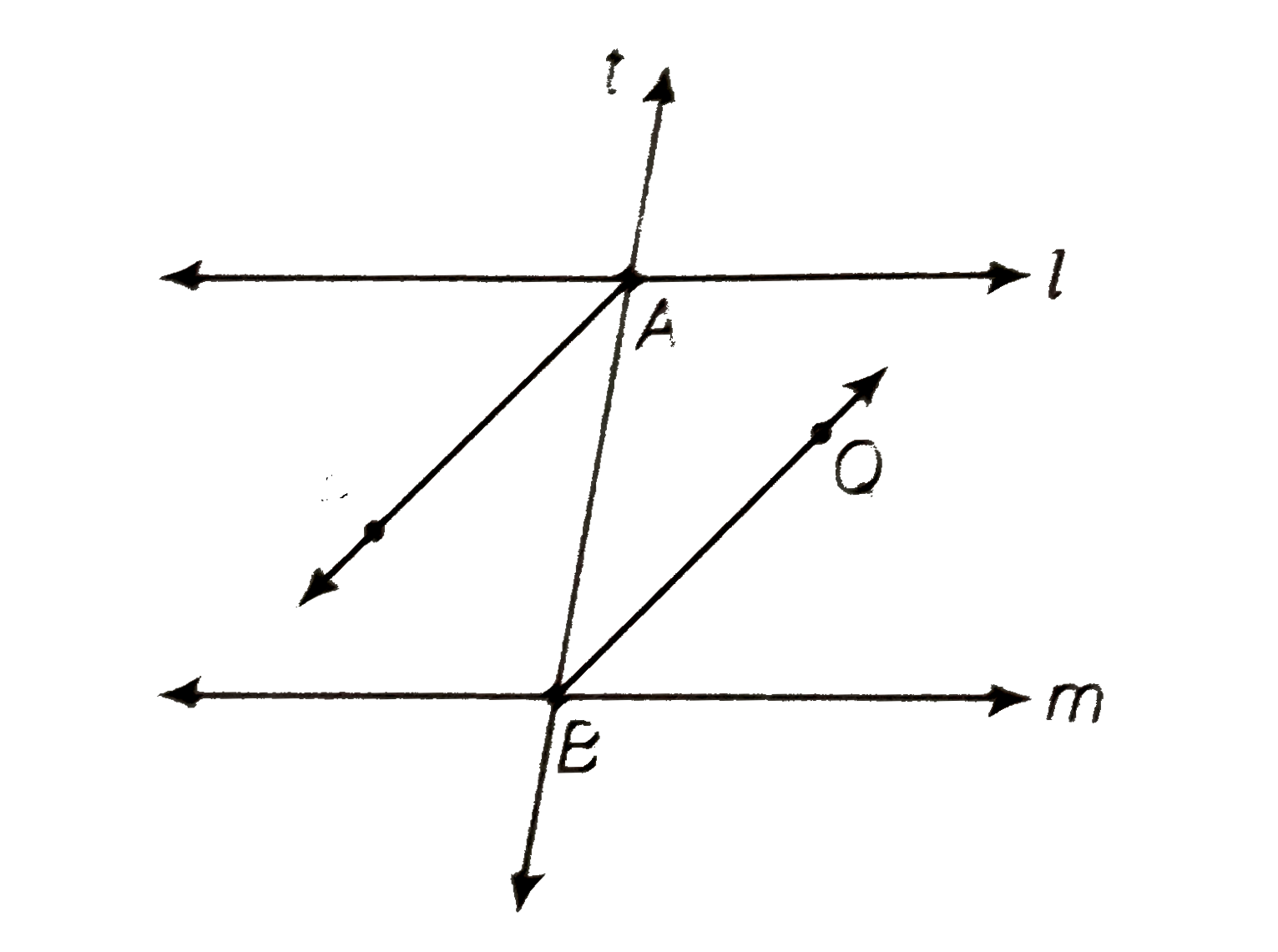 View Solution
View SolutionIf a transversal intersects two parallel lines, then
alternate interior angles are on the _______ side of the transversal.View SolutionIf the bisectors of a pair of corresponding angles formed by a transversal with two given lines are parallel;prove that the given lines are parallel.
View Solution

