Question

If the graphs of the functions${\displaystyle y={\log }_{e}x\text{and}y=ax}$ intersect at exactly two points,then find the value of ${\displaystyle a}$.

Explanation

Given curves are `y=log_(e)x and y =ax`.
We want the value of a for which `log_(e)x= ax` has exactly two solutions.
Let us first find the vlaues of x for which `y=ax` is tangent to `y=log_(e)x`,
For `" "y=log_(e)x, (dy)/(dx)=(1)/(x)`
We must have `(1)/(x) =a therefore y=1, x=e and a= (1)/(e)`.
Thus, the line `y= (x)/(e)` touches `y= log_(e)x` as shown in the following figure.

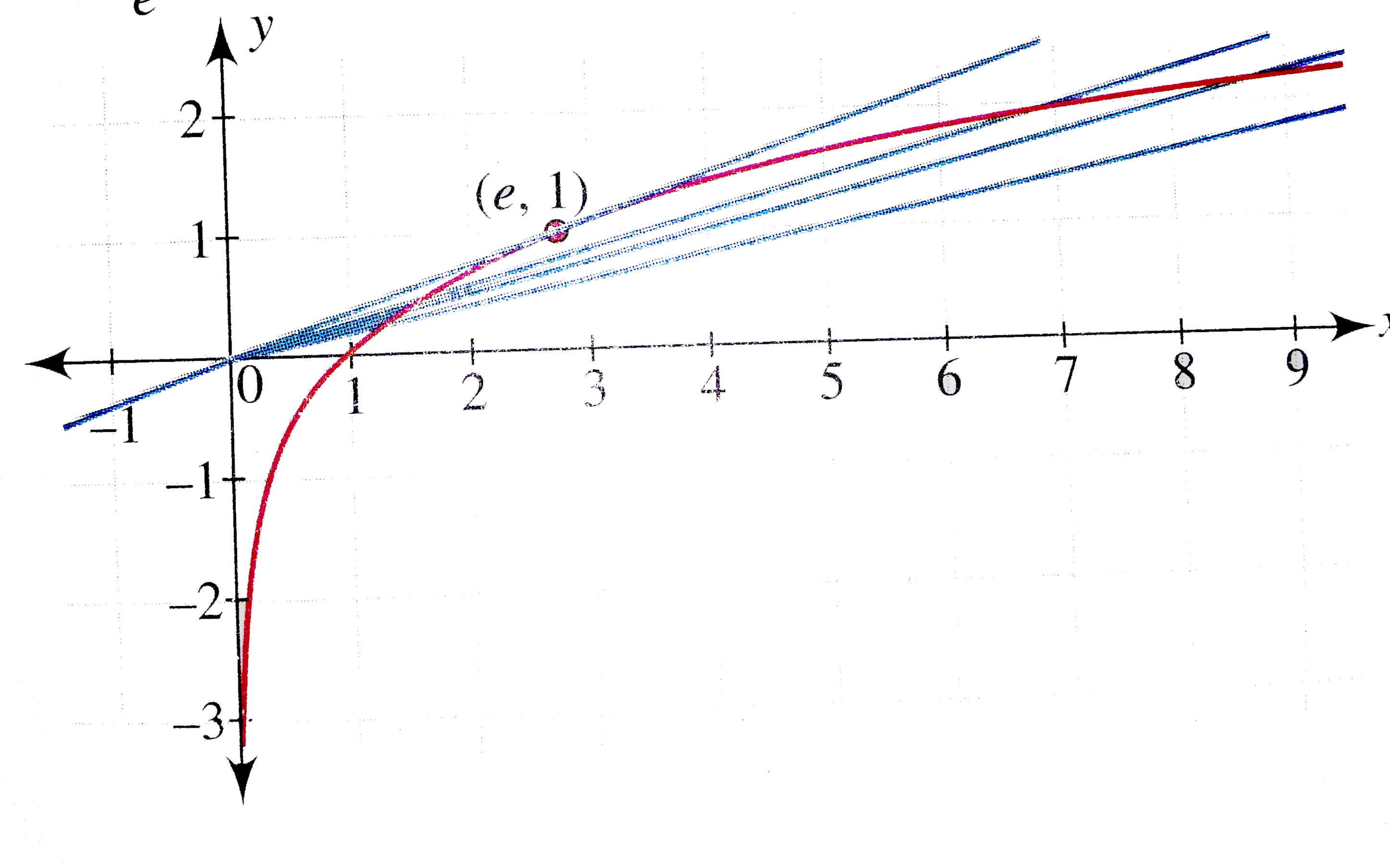
Line `y=ax` intersect `y=log_(e)x` in two points if its slope is less than `(1)/(e)` and line must cut the curve in first quadrant only.
Hence `a in (0, (1)/(e))`.