If the mean deviation about the median of the numbers a, 2a ,…., 50 a is 50 then |a| equals
2
3
4
5
The correct Answer is:C
To solve the problem, we need to find the value of |a| given that the mean deviation about the median of the numbers a, 2a, ..., 50a is 50.
1. Identify the Series: The given series is a, 2a, 3a, ..., 50a. This is an arithmetic series with 50 terms.
2. Find the Median:
- Since there are 50 terms (even number), the median is the average of the 25th and 26th terms.
- The 25th term is 25a and the 26th term is 26a.
- Therefore, the median M is:
M=25a+26a2=51a2
3. Calculate the Mean Deviation:
- The mean deviation about the median is given by the formula:
Mean Deviation=∑|xi−M|n
- Here, n=50 and M=51a2.
- We need to calculate |xi−M| for each term xi in the series.
4. Compute |xi−M|:
- For xi=ka where k=1,2,...,50:
|xi−M|=∣∣∣ka−51a2∣∣∣=∣∣∣a(k−512)∣∣∣=|a||k−25.5|
5. Sum of Deviations:
- We need to calculate ∑|xi−M|:
∑|xi−M|=|a|50∑k=1|k−25.5|
- The sum 50∑k=1|k−25.5| can be split into two parts:
- For k=1 to 25: |k−25.5|=25.5−k
- For k=26 to 50: |k−25.5|=k−25.5
6. Calculate Each Part:
- For k=1 to 25:
25∑k=1(25.5−k)=25.5×25−25∑k=1k=637.5−25×262=637.5−325=312.5
- For k=26 to 50:
50∑k=26(k−25.5)=50∑k=26k−25.5×25=50×512−25.5×25=1275−637.5=637.5
7. Total Sum of Deviations:
- Therefore, the total sum is:
∑|xi−M|=|a|(312.5+637.5)=|a|×950
8. Mean Deviation Calculation:
- Now, substituting back into the mean deviation formula:
Mean Deviation=|a|×95050=19|a|
- We know from the problem statement that this mean deviation equals 50:
19|a|=50
9. Solve for |a|:
- Rearranging gives:
|a|=5019
Final Answer:
|a|=5019
- Since there are 50 terms (even number), the median is the average of the 25th and 26th terms.
- The 25th term is 25a and the 26th term is 26a.
- Therefore, the median M is:
M=25a+26a2=51a2
- The mean deviation about the median is given by the formula:
Mean Deviation=∑|xi−M|n
- Here, n=50 and M=51a2.
- We need to calculate |xi−M| for each term xi in the series.
- For xi=ka where k=1,2,...,50:
|xi−M|=∣∣∣ka−51a2∣∣∣=∣∣∣a(k−512)∣∣∣=|a||k−25.5|
- We need to calculate ∑|xi−M|:
∑|xi−M|=|a|50∑k=1|k−25.5|
- The sum 50∑k=1|k−25.5| can be split into two parts:
- For k=1 to 25: |k−25.5|=25.5−k
- For k=26 to 50: |k−25.5|=k−25.5
- For k=1 to 25:
25∑k=1(25.5−k)=25.5×25−25∑k=1k=637.5−25×262=637.5−325=312.5
- For k=26 to 50:
50∑k=26(k−25.5)=50∑k=26k−25.5×25=50×512−25.5×25=1275−637.5=637.5
- Therefore, the total sum is:
∑|xi−M|=|a|(312.5+637.5)=|a|×950
- Now, substituting back into the mean deviation formula:
Mean Deviation=|a|×95050=19|a|
- We know from the problem statement that this mean deviation equals 50:
19|a|=50
- Rearranging gives:
|a|=5019
|a|=5019
Topper's Solved these Questions
- MEASURES OF CENTRAL TENDENCY BOOK - ML KHANNACHAPTER - MEASURES OF CENTRAL TENDENCY EXERCISE - ASSERTION / REASON
1 Videos
- MEASURES OF CENTRAL TENDENCY BOOK - ML KHANNACHAPTER - MEASURES OF CENTRAL TENDENCY EXERCISE - Problem Set (1) (Measures of Disperation)
23 Videos
- MAXIMA AND MINIMA BOOK - ML KHANNACHAPTER - MAXIMA AND MINIMA EXERCISE - MISCELANEOUS EXERCISE (COMPREHENSION)
3 Videos
- NUMERICAL METHODSBOOK - ML KHANNACHAPTER - NUMERICAL METHODSEXERCISE - SELF ASSESSMENT TEST
10 Videos
Similar Questions
Knowledge Check
If the mean deviation about the median of the numbers a, 2a ,…., 50 a is 50 then |a| equals
A3B4C5D2
The mean deviation about the median of the numbers 2, 3, 5, 20, 17, 15, 11, 9, 7 is
View SolutionIf the mean deviation about mean of the numbers x,2x,3x,...,29x,x>0 is 42029 then x equals
View SolutionFind the mean deviation about the mean of the distributon .

View SolutionFind the mean deviation about the mean of the distributon .

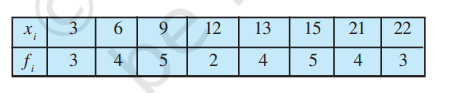
View SolutionFind the mean deviation about the median for the following data:
View SolutionFind the mean deviation about the mean for the following data.

View SolutionFind the mean deviation about the mean for the following data :

View Solution

