IF THE MINIMUM VALUE OF AN OBJECTIVE FUNCTION Z=ax+by occurs at two point(3,4) and 4,3
15
−15
21
can't be determine
The correct Answer is:A
To solve the problem, we need to find the minimum value of the objective function Z=ax+by given that it occurs at two points: (3, 4) and (4, 3).
1. Understanding the Objective Function:
The objective function is given as Z=ax+by. We need to find the coefficients a and b such that the minimum value occurs at the specified points.
2. Substituting the Points into the Objective Function:
We will substitute the points (3, 4) and (4, 3) into the objective function:
- For point (3, 4):
Z1=a(3)+b(4)=3a+4b
- For point (4, 3):
Z2=a(4)+b(3)=4a+3b
3. Setting the Objective Function Values Equal:
Since both points yield the minimum value of Z, we can set the two expressions for Z equal to each other:
3a+4b=4a+3b
4. Rearranging the Equation:
Rearranging the equation gives:
3a+4b−4a−3b=0
Simplifying this leads to:
−a+b=0⇒b=a
5. Finding the Minimum Value:
Now that we have b=a, we can substitute b back into either equation to find the minimum value. Let's use b=a in Z1:
Z=3a+4b=3a+4a=7a
The minimum value of Z depends on the value of a.
6. Conclusion:
The minimum value of the objective function Z occurs at both points (3, 4) and (4, 3) and is given by Z=7a, where a can be any real number.
The objective function is given as Z=ax+by. We need to find the coefficients a and b such that the minimum value occurs at the specified points.
We will substitute the points (3, 4) and (4, 3) into the objective function:
- For point (3, 4):
Z1=a(3)+b(4)=3a+4b
- For point (4, 3):
Z2=a(4)+b(3)=4a+3b
Since both points yield the minimum value of Z, we can set the two expressions for Z equal to each other:
3a+4b=4a+3b
Rearranging the equation gives:
3a+4b−4a−3b=0
Simplifying this leads to:
−a+b=0⇒b=a
Now that we have b=a, we can substitute b back into either equation to find the minimum value. Let's use b=a in Z1:
Z=3a+4b=3a+4a=7a
The minimum value of Z depends on the value of a.
The minimum value of the objective function Z occurs at both points (3, 4) and (4, 3) and is given by Z=7a, where a can be any real number.
Topper's Solved these Questions
- QUADRATIC EQUATIONS BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - QUADRATIC EQUATIONS EXERCISE - EXERCISE (MATCHING TYPE PROBLEMS)
1 Videos
- QUADRATIC EQUATIONS BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - QUADRATIC EQUATIONS EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
45 Videos
- QUADRATIC EQUATIONS BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - QUADRATIC EQUATIONS EXERCISE - EXERCISE (ONE OR MORE THAN ONE ANSWER IS/ARE CORRECT)
44 Videos
- PROBABILITY BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - PROBABILITY EXERCISE - Exercise -5 : Subjective Type problems
12 Videos
- SEQUENCE AND SERIES BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
21 Videos
Similar Questions
The corner points of the feasible region of a system of linear inequalities are (0, 0), (4,0), (3,9), (1, 5) and (0, 3). If the maximum value of objective function, Z = ax + by occurs at points (3, 9) and (1, 5), then the relation between a and b is:
View SolutionFind the distance of point (−1,−3,4) from x,y and z-axes.
View Solution
Knowledge Check
The corner points of the feasible region determined by a system of linear inequations are (0,0),(4,0),(2,4) and (0,5). If the minimum value of Z=ax+by,a, b>0 occurs at (2,4) and (0,5) ,then :
Aa=2bB2a=bCa=bD3a=bConsider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
Which of the following statements are true?AI and IVBII and IIICI and IIIDII and IVLet f(x) = 4x2−4ax+a2−2a+2 and the golbal minimum value of f(x) for x in [0,2] is equal to 3
The number of values of a for which the global minimum value equal to 3 for x in [0,2] occurs at the endpoint of interval[0,2] isA1B2C3D0
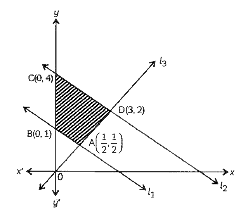
The feasible region of a system of linear inequalities is shown shaded in the following graph . If the objective function is Z = ax + by where a,b are constants and the maximum of Z occurs at points A and D then :
View SolutionMaximum value of the objective function Z = ax +by in a LPP always occurs at only one corner point of the feasible region.
View SolutionP is a point satisfying arg z=π4, such that sum of its distance from two given points (0,1) and (0,2) is minimum, then P must be k3(1+i) . Then numerical value of k is
View SolutionMinimize z=2x+4y is subjected to 2x+y≥3,x+2y≥6,x≥0,y≥0 show that the minimum value of z occurs at more than two points
View SolutionLet R be the feasible region (convex polygon) for a linear programming problem and Z = ax + by be the objective function. Then, which of the following statements is false?
View Solution
