If the point is symmetric to the point with respect to the bisector of the first quadrant then is
The correct Answer is:B
To solve the problem, we need to find the distance AB where point A is symmetric to point B(4,−1) with respect to the bisector of the first quadrant, which is the line y=x.
1. Identify the coordinates of point B:
Given point B is (4,−1).
2. Determine the symmetric point A:
The line y=x bisects the first quadrant. To find the symmetric point A of point B with respect to this line, we swap the x-coordinate and y-coordinate of point B. Thus, the coordinates of point A will be:
A=(−1,4)
3. Use the distance formula to find AB:
The distance AB between points A(x1,y1) and B(x2,y2) can be calculated using the distance formula:
AB=√(x2−x1)2+(y2−y1)2
Here, A(−1,4) and B(4,−1). So, substituting the coordinates:
AB=√(4−(−1))2+(−1−4)2
Simplifying the expression:
AB=√(4+1)2+(−1−4)2
AB=√(5)2+(−5)2
AB=√25+25
AB=√50
AB=5√2
4. Final Answer:
The distance AB is 5√2.
Given point B is (4,−1).
The line y=x bisects the first quadrant. To find the symmetric point A of point B with respect to this line, we swap the x-coordinate and y-coordinate of point B. Thus, the coordinates of point A will be:
A=(−1,4)
The distance AB between points A(x1,y1) and B(x2,y2) can be calculated using the distance formula:
AB=√(x2−x1)2+(y2−y1)2
Here, A(−1,4) and B(4,−1). So, substituting the coordinates:
AB=√(4−(−1))2+(−1−4)2
Simplifying the expression:
AB=√(4+1)2+(−1−4)2
AB=√(5)2+(−5)2
AB=√25+25
AB=√50
AB=5√2
The distance AB is 5√2.
Topper's Solved these Questions
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Section-1 Solved MCQs (Example)
1 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - SECTION - II (ASSERTION - REASON TYPE MCQs)
14 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ILLUSTRATION 18
1 Videos
- SETSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Chapter Test
30 Videos
Similar Questions
If the point A is symmetric to the point B(4,−1) with respect to the bisector of the first quadrant, then the length of AB is:
View SolutionLet A≡(−4,0),B≡(−1,4).CandD are points which are symmetric to points AandB respectively with respect to y-axis, then area of the quadrilateral ABCD is (A) 8 sq units (B) 12 sq. units (C) 20 sq. units (D) none of these
View SolutionFigure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.
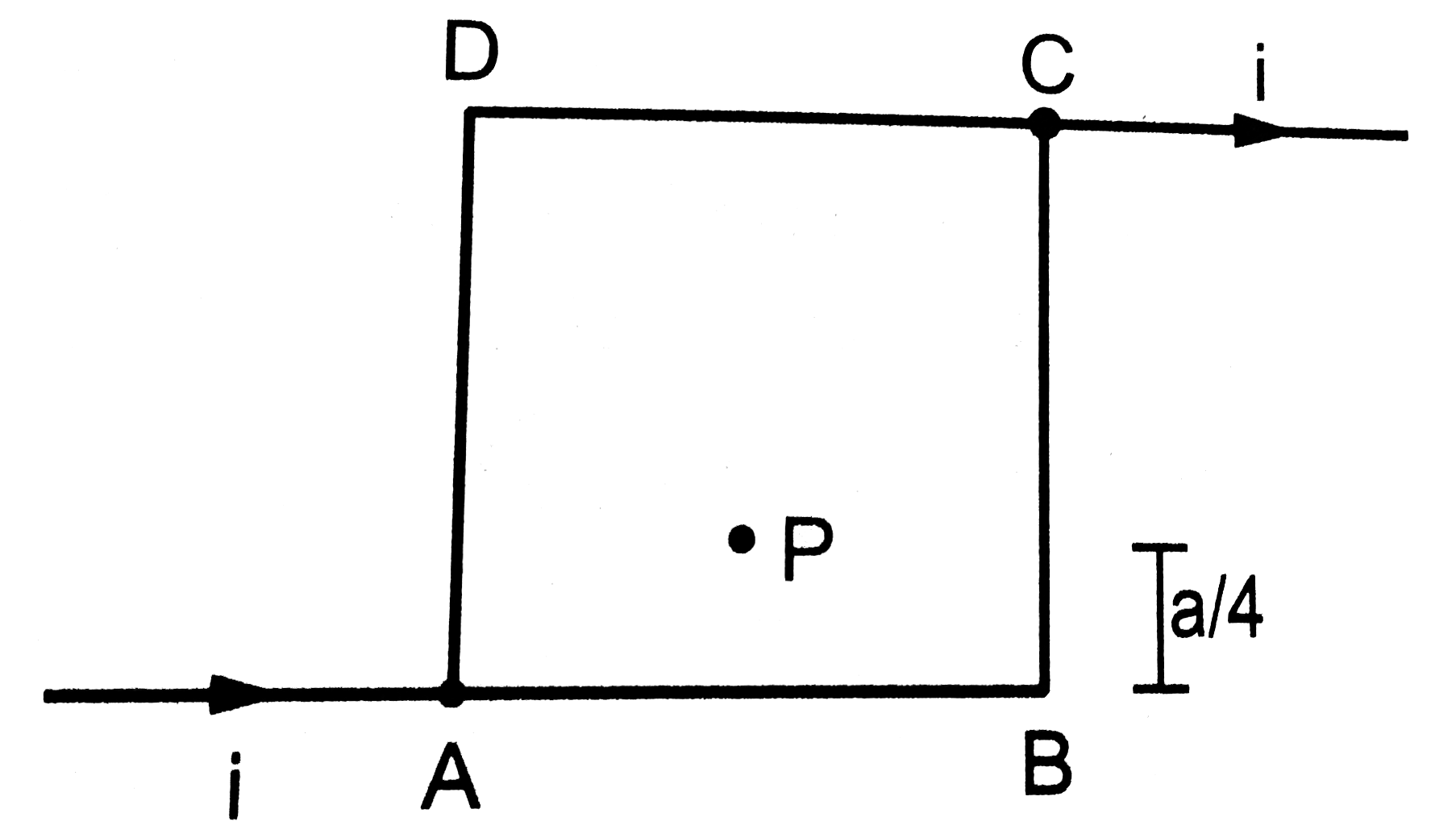
View SolutionA(-4,0) and B (-1,4) are two given points. Cand D are points which are symmetric to the given points A and B respectively with respect to y-axis. Calculate the perimeter of the trapezium ABDC.
View SolutionState, true or false:
If the ordinate of a point is equal to its abscissa, the point lies either in the first quadrant or in the second quadrant.
View SolutionTangent drawn from the point P(4,0) to the circle x2+y2=8 touches it at the point A in the first quadrant. Find the coordinates of another point B on the circle such that AB=4 .
View SolutionA circle is passing through the points A (1, 1) and B (1, 3) and the bisector of first and third quadrant is normal to it, then its area is
View SolutionIf A is symmetric matrix, then B'AB is............
View SolutionFind the coordinates of the point Q on the X- axis which lies on the perpendicular bisector of the line segment joining the points A (-5,-2) and B (4,-2). Name the type of triangle formed by the points Q , A and B.
View SolutionStatement - 1 : If the perpendicular bisector of the line segment joining points A (a,3) and B( 1,4) has y-intercept -4 , then a=±4.
Statement- 2 : Locus of a point equidistant from two given points is the perpendicular bisector of the line joining the given points .
View Solution
