If the point A is symmetric to the point B(4,−1) with respect to the bisector of the first quadrant, then the length of AB is:
5
5√2
3√2
3
The correct Answer is:B
To find the length of segment AB, where point A is symmetric to point B(4, -1) with respect to the bisector of the first quadrant (the line x = y), we can follow these steps:
1. Identify the Bisector: The bisector of the first quadrant is the line where x = y. This line divides the first quadrant into two equal halves.
2. Coordinates of Point B: The coordinates of point B are given as B(4, -1).
3. Determine the Symmetric Point A: To find the coordinates of point A, we need to reflect point B across the line x = y. The reflection of a point (x, y) across the line x = y is given by (y, x). Therefore, reflecting point B(4, -1):
- The x-coordinate of A will be the y-coordinate of B: -1.
- The y-coordinate of A will be the x-coordinate of B: 4.
- Thus, the coordinates of point A are A(-1, 4).
4. Calculate the Length of AB: The length of segment AB can be calculated using the distance formula:
AB=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of A and B:
AB=√((−1)−4)2+(4−(−1))2
=√(−5)2+(5)2
=√25+25
=√50
=5√2
5. Final Result: The length of AB is 5√2.
- The x-coordinate of A will be the y-coordinate of B: -1.
- The y-coordinate of A will be the x-coordinate of B: 4.
- Thus, the coordinates of point A are A(-1, 4).
AB=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of A and B:
AB=√((−1)−4)2+(4−(−1))2
=√(−5)2+(5)2
=√25+25
=√50
=5√2
Topper's Solved these Questions
- STRAIGHT LINESBOOK - VMC MODULES ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Level -2
43 Videos
- STRAIGHT LINESBOOK - VMC MODULES ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Level -2 Passage
5 Videos
- STRAIGHT LINESBOOK - VMC MODULES ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Level - 0 (True or False)
7 Videos
- SEQUENCE AND SERIES BOOK - VMC MODULES ENGLISHCHAPTER - SEQUENCE AND SERIES EXERCISE - JEE MAIN & Advance ( ARCHIVE)
46 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - VMC MODULES ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - JEE ADVANCED (ARCHIVE)
34 Videos
Similar Questions
If the point A is symmetric to the point B(4,−1) with respect to the bisector of the first quadrant then AB is
View SolutionLet A≡(−4,0),B≡(−1,4).CandD are points which are symmetric to points AandB respectively with respect to y-axis, then area of the quadrilateral ABCD is (A) 8 sq units (B) 12 sq. units (C) 20 sq. units (D) none of these
View SolutionThe position verctors of the points A and B with respect of O are 2ˆi+2ˆj+ˆkand2ˆi+4ˆj+4ˆk, the length of the internal bisector of ∠BOA of ΔAOB is
View SolutionCircles are drawn through the point (2, 0) to cut intercept of length 5 units on the x-axis. If their centers lie in the first quadrant, then find their equation.
View SolutionA(-4,0) and B (-1,4) are two given points. Cand D are points which are symmetric to the given points A and B respectively with respect to y-axis. Calculate the perimeter of the trapezium ABDC.
View SolutionA circle is passing through the points A (1, 1) and B (1, 3) and the bisector of first and third quadrant is normal to it, then its area is
View SolutionTangent drawn from the point P(4,0) to the circle x2+y2=8 touches it at the point A in the first quadrant. Find the coordinates of another point B on the circle such that AB=4 .
View SolutionIn which quadrant do the points lie: (4,3)
View SolutionPoint A and B are in the first quadrant; point O is the origin. If the slope of OA is 1, the slope of OB is 7, and OA=OB, then the slope of AB is −15 (b) −14 (c) −13 (d) −12
View SolutionFigure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.
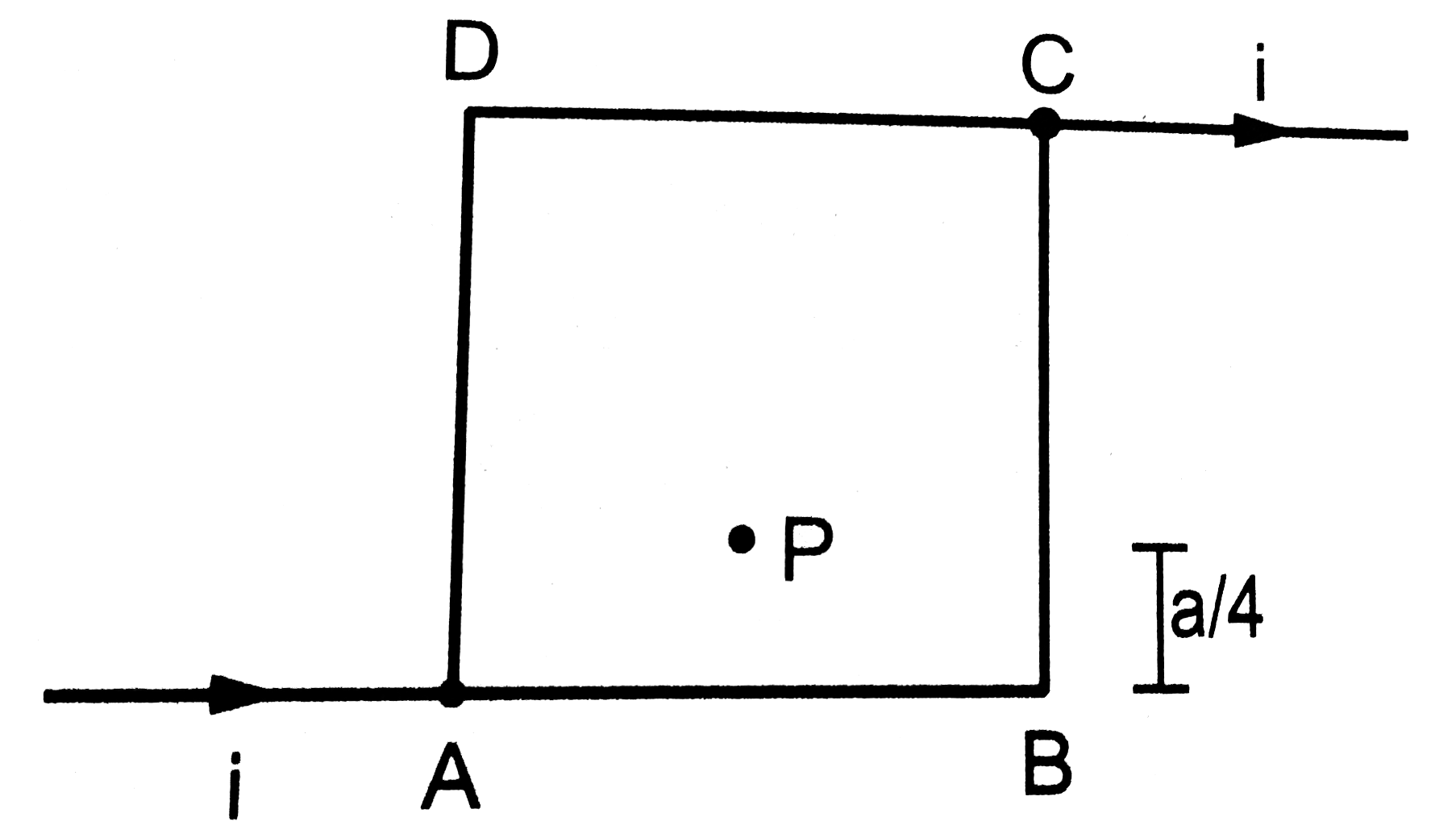
View Solution