If the polynomial equation anxn+an−1xn−1+an−2xn−2+.......+a0=0,n being a positive integer, has two different real roots a and b. then between a and b the equation nanxn−1+(n−1)an−1xn−2+.......+a1=0 has
exactly one root
almost one root
at least one root
no root
The correct Answer is:C
Step by step video & image solution for If the polynomial equation a_n x^n + a_(n-1) x^(n-1) + a_(n-2) x^(n-2) + ....... + a_0 = 0, n being a positive integer, has two different real roots a and b. then between a and b the equation na_n x^(n-1) +(n-1)a_(n-1) x^(n-2) +.......+a_1 =0 has by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MEAN VALUE THEOREMSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MEAN VALUE THEOREMSEXERCISE - Section II - Assertion Reason Type
4 Videos
- MATRICESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATRICESEXERCISE - Chapter Test
30 Videos
- PAIR OF STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Chapter Test
18 Videos
Similar Questions
Knowledge Check
If an+1=an−1+2an for n=2,3,4,... and a1=1 and a2=1, then a5=
A7B11C17D21
In the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.
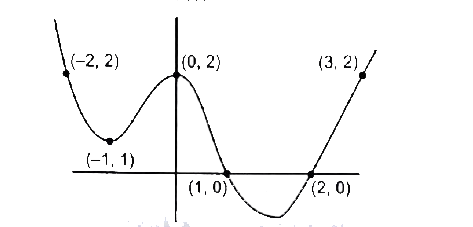
The product of all imaginary roots of p(x)=0 is:
View SolutionIf a1,a2,a3......an(n≥2) are real and (n−1)a21−2na2<0 then prove that at least two roots of the equation xn+a1xn−1+a2xn−2+......+an=0are imaginary.
View SolutionLet a1,a2,a3,...an be an AP. then: 1a1an+1a2an−1+1a3an−2+......+1ana1=
View SolutionIn the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.
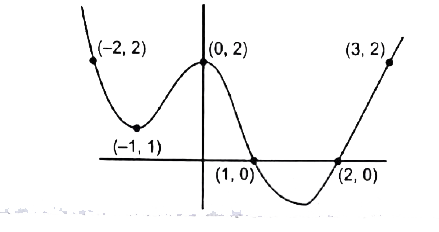
The minimum number of real roots of equation (p'(x))2+p(x)p''(x)=0 are:
View SolutionIf a1,a2 …. an are positive real numbers whose product is a fixed real number c, then the minimum value of 1+a1+a2 +….. + an−1+an is :
View SolutionLet n be a positive integer and (1+x+x2)n=a0+a1x+....+a2nx2n.
Show that a02−a12+a22+...+a2n2=an
View SolutionConsider (1+x+x2)n=2n∑r=0arxr,where a0,a1,
a2,…a2n are real numbers and n is a positive integer.
The value of a2 is
View Solution
