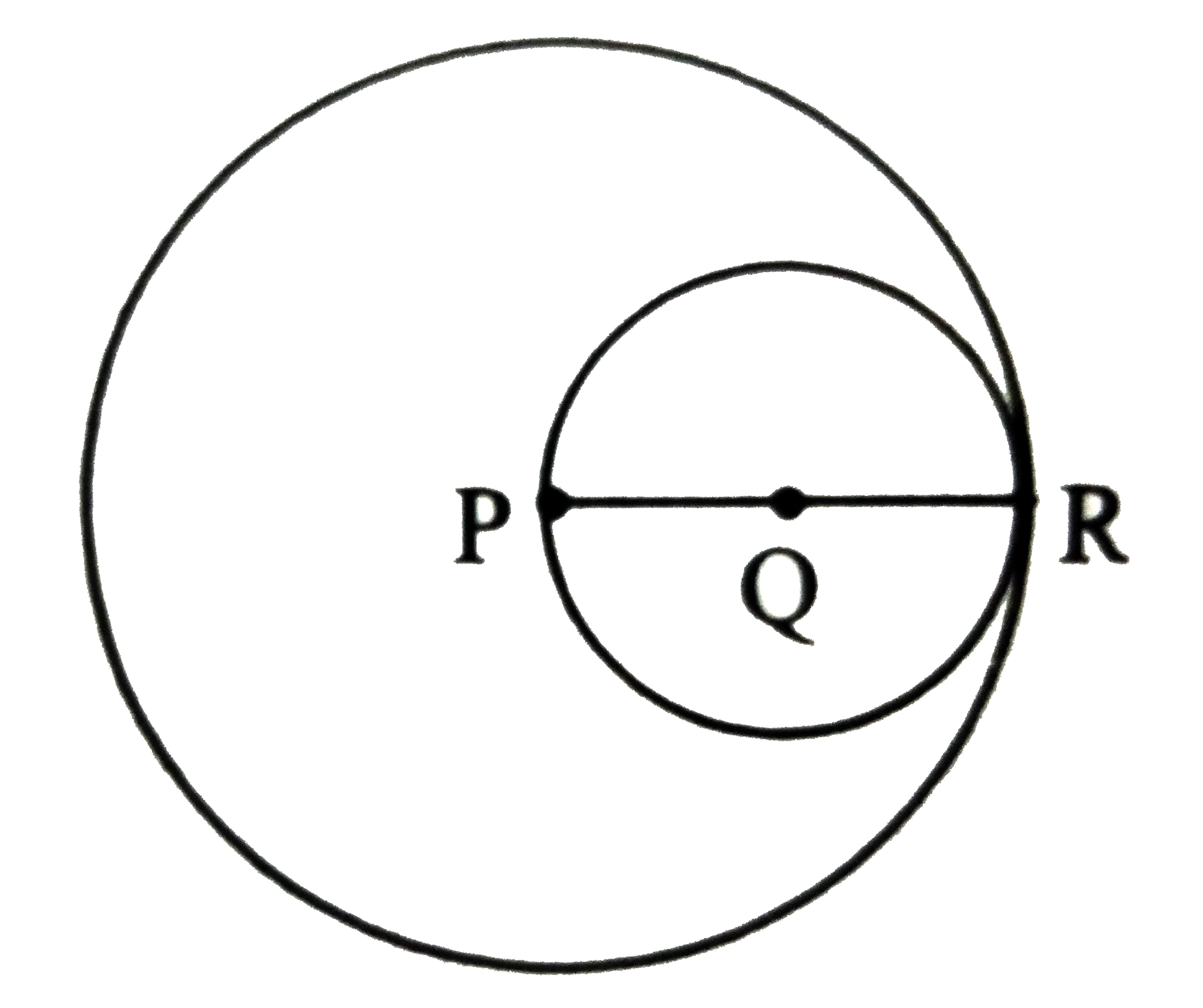
IF two circles of radii $r_{1}$ and $r_{2}$ $(r_{2} > r_{1})$ touch internally , then the distance between their centres will be

A

$r_{1} - r_{2}$

B

$r_{2} - r_{1}$

C

$r_{1}^{2} - r_{2}^{2}$

D

$r_{2}^{2} - r_{1}^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

|

Answer

Step by step video, text & image solution for IF two circles of radii r_1 and r_2 (r_2gtr_1) touch internally , then the distance between their centres will be by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two circles of radii 13 cm and 5 cm touch internally each other. Find the distance between their centres:
A18 cm
B12 cm
C9 cm
D8 cm
Question 2 - Select One
Two circles of radii 13 cm and 5 cm touch internally each other. Find the distance between their centres:
A18 cm
B12 cm
C9 cm
D8 cm
Question 3 - Select One
Two circles of radii $r_{1}$ and $r_{2}, r_{1} > r_{2} \geq 2$ touch each other externally. If $θ$ be the angle between the direct common tangents, then,
A $θ = {sin}^{- 1} (\frac{r_{1} + r_{2}}{r_{1} - r_{2}})$
B $θ = 2 {sin}^{- 1} (\frac{r_{1} - r_{2}}{r_{1} + r_{2}})$
C $θ = {sin}^{- 1} (\frac{r_{1} - r_{2}}{r_{1} + r_{2}})$
Dnone of these

TARGET PUBLICATION-CIRCLE-Multiple Choice Question

Home
Ask Doubt
Profile