Angles inscribed in the same arc are
congruent
complementary
supplementary
none of these
The correct Answer is:A
Topper's Solved these Questions
- CIRCLEBOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Additional Problems for Practice
32 Videos
- CIRCLEBOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Chapter Assessment
9 Videos
- CIRCLEBOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Activities for Practice
4 Videos
- CHALLENGING QUESTIONS BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - Chapter 6: Statistics
4 Videos
- CO-ORDINATE GEOMETRYBOOK - TARGET PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - CHAPTER ASSESSMENT
19 Videos
Similar Questions
Knowledge Check
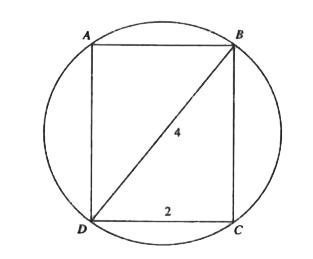
In the figure, ABCD is a rectangle inscribed in the circle shown. What is the length of the smaller arc DC ?
 Aπ/4B2π/3Cπ/2D3π/4
Aπ/4B2π/3Cπ/2D3π/4ABC is an equilateral triangle inscribed in a circle. D is any point on the arc BC. What is ∠ADB equal to?
A90∘B60∘C45∘DNone of these
Prove that an angle inscribed in a semi-circle is a right angle using vector method.
View SolutionProve that an angle inscribed in a semi-circle is a right angle using vector method.
View SolutionAn equilateral triangle ABC and a scalene triangle DBC are inscribed in a circle on same side of the arc. What is ∠BDC equal to?
View SolutionInscribed Angle Theorem
The measure of an inscribed angle is half of the measure of the arc intercepted by it.
Given : In a circle with centre O, ∠BAC is inscribed in an arc BAC. ∠BAC intercepts are BXC of the circle.
To prove :m∠BAC=12 m ( arc BXC ) .
View SolutionIn the given figure, one side of the 30∘ inscribed angle is the diameter of a semicircle of radius 3 cm. What is the perimeter of the shaded region bounded by the inscribed angle and its intercepted arc
View SolutionIn the figures, ∠ABC is inscribed in arc ABC and intercepts arc AXC and ∠BCD is inscribed in arc BCD and intercepts arc BYD. If ∠ABC=30∘ and m ( arc BYD ) =80∘ then the m ( arc AXC ) = ….... and measure of ∠BCD=….........

View Solution