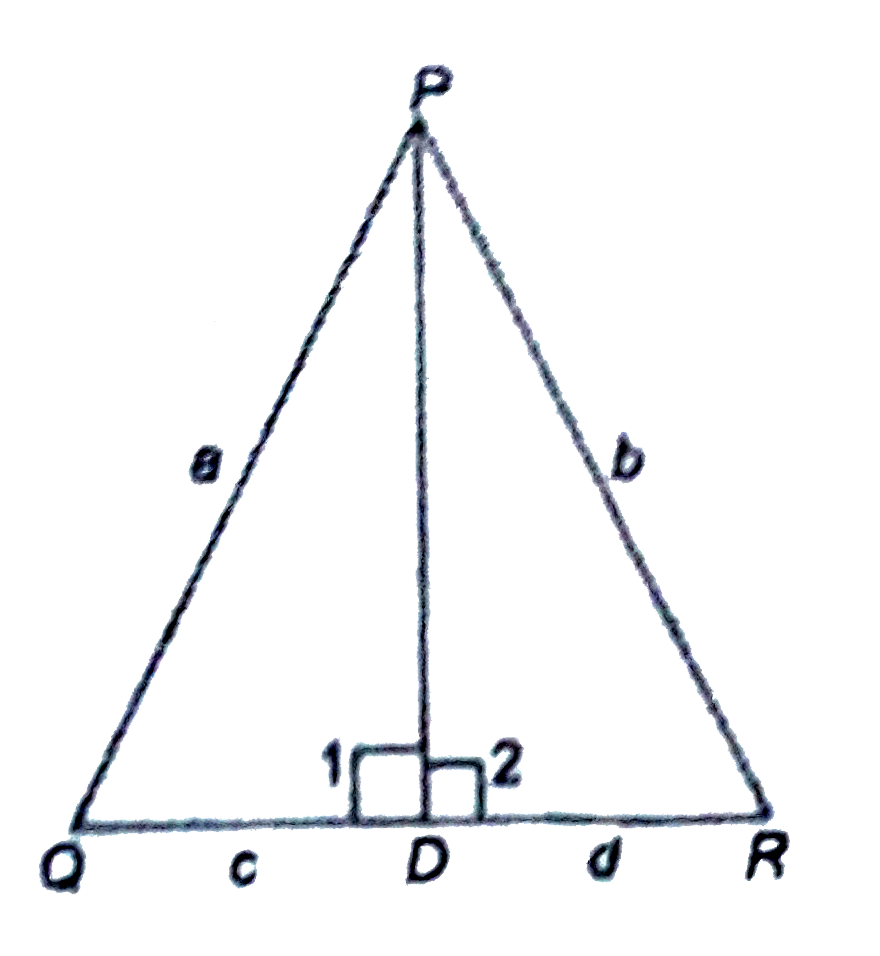
Ii ΔPQR, PD⊥QR such that D lies on QR, if PQ=a,PR=b,QD=c and DR=d, then prove that (a+b)(a-b)=(c+d)(c-d).
Video Solution
Text Solution
Given: In △PQR,PD⊥QR,so∠1=∠2
PQ=a,PR=b,QD=c and DR=d
To prove: (a+b) (a-b) = (c+d) (c-d)
Proof : in right angle △PDQ
PD2=PQ2−QD2 (by pythagoras theorem)
⇒ PD2=a2−c2 ...(1)
similarlym in right angled △PDR
PD2=PR2−DR2 ( by pythagoras theorem) (by pythagoras theorem )
PD2=b2−d2
From (1) and (2) ,we have
a2−c2=b2−d2
a2−b2=c2−d2
(a-b) (a+b) = (c-d) (c+d) Hence proved.
|
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6a
23 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Eercise 6b
1 Video
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Revision Exercise Long Questions
4 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
Knowledge Check
Ii ΔPQR, PD⊥QR such that D lies on QR, if PQ=a,PR=b,QD=c and DR=d, then prove that (a+b)(a-b)=(c+d)(c-d).
A(a−d)(a+d)=(b−c)(b+c)B(a−c)(b−d)=(a+c)(b+d)C(a−b)(a+b)=(c+d)(c−d)D(a−b)(c−d)=(a+b)(c+d)
If a, b, c, d are in G.P., then prove that:
(b−c)2+(c−a)2+(d−b)2=(a−d)2
View SolutionIf a,b,c,d are in GP then prove that a+b,b+c,c+d are in GP.
View SolutionIn ΔPQR,PQ=QR,m∠PQR=120∘,Qd⊥PR,P−D−R then prove that
mPR=√3QR=√3PQ
View SolutionIf a, b, c, d are in GP, prove that
(b−c)2+(c−a)2+(d−b)2=(a−d)2.
View SolutionIn Fig. 5.10, if AC=BD, then prove that AB=CD.

View SolutionIf a, b, c and d are four coplanr points, then prove that [abc]=[bcd]+[abd]+[cad].
View SolutionIf A={a,b},B={c,d},C={d,e} then {(a,c),(a,d),(a,e),(b,c),(b,d),(b,e)}=
View Solution