In Figure altitudes AD and CE of △ABC
intersect each other at the point P. Show that:
(i) ΔAEP~ΔCDP
(ii) ΔABD~ΔCBE
(iii) ΔAEP~ΔADB
(iv) ΔPDC~ΔBEC
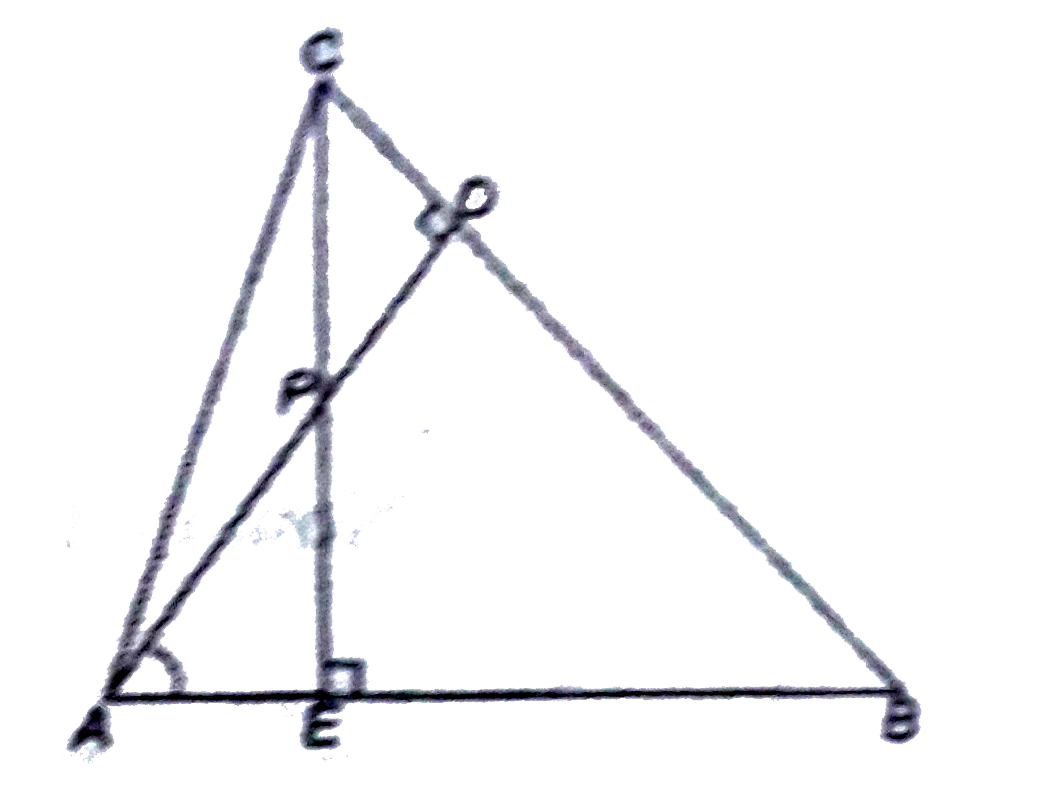
(i) in figure, ∠AEP=∠CDP (each=90∘
and ∠APE=∠CPD ( vertically opposite angles)
⇒ △AEP~△CDP (by AAA similarity critertion)
Hence proved
(ii)figure,∠ADB=∠CEB (each=90∘)
and ∠ABD=∠CBE ( by AAA similarity criterion) Hence proved.
( iii) in figure, ∠AEP=∠ADB (each90∘)
and∠PAE=∠BAD (common angle)
⇒ △AEP~△ADB ( by AAA similarity criterion ) Hence proved.
(iv) in figure , ∠PDC=∠BEC(each=90∘)
and ∠PCD=∠BCE ( common angle)
⇒ △PDC~△BEC ( by AAA similarity criterion) Hence proved.

Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6a23videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Eercise 6b1videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Revision Exercise Long Questions4videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions5videos
STATISTICS
- BOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions5videos
VOLUME AND SURFACE AREA OF SOLIDS
Similar Questions
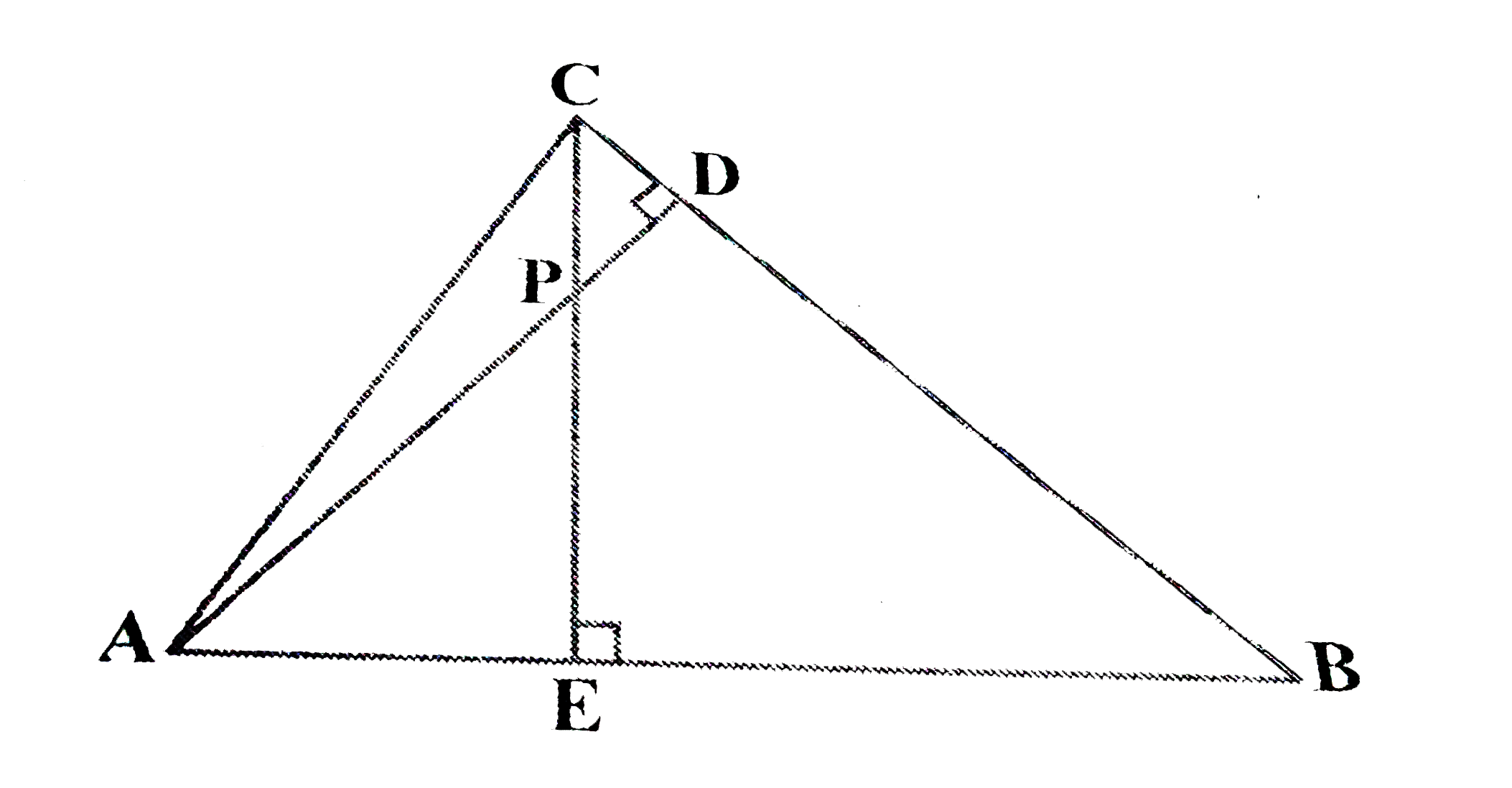
In Figure altitudes AD and CE of DABC intersect each other at the point P. Show that:
(i) ΔAEP~ΔCDP
(ii) ΔABD~ΔCBE
(iii) ΔAEP~ΔADB
(iv) ΔPDC~ΔBEC
 View Solution
View SolutionIn Figure, two chords AB and CD intersect each other at the point P. Prove that:
(i) ΔAPC~ΔDPB
(ii) AP⋅PB=CP⋅DP
 View Solution
View SolutionIn Figure two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC~ΔPDB
(ii) PA.PB=PC.PD
 View Solution
View SolutionIn figure, if ΔABE≅ΔACD, show that ΔADE~ΔABC.
 View Solution
View SolutionE is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE~ΔCFB.
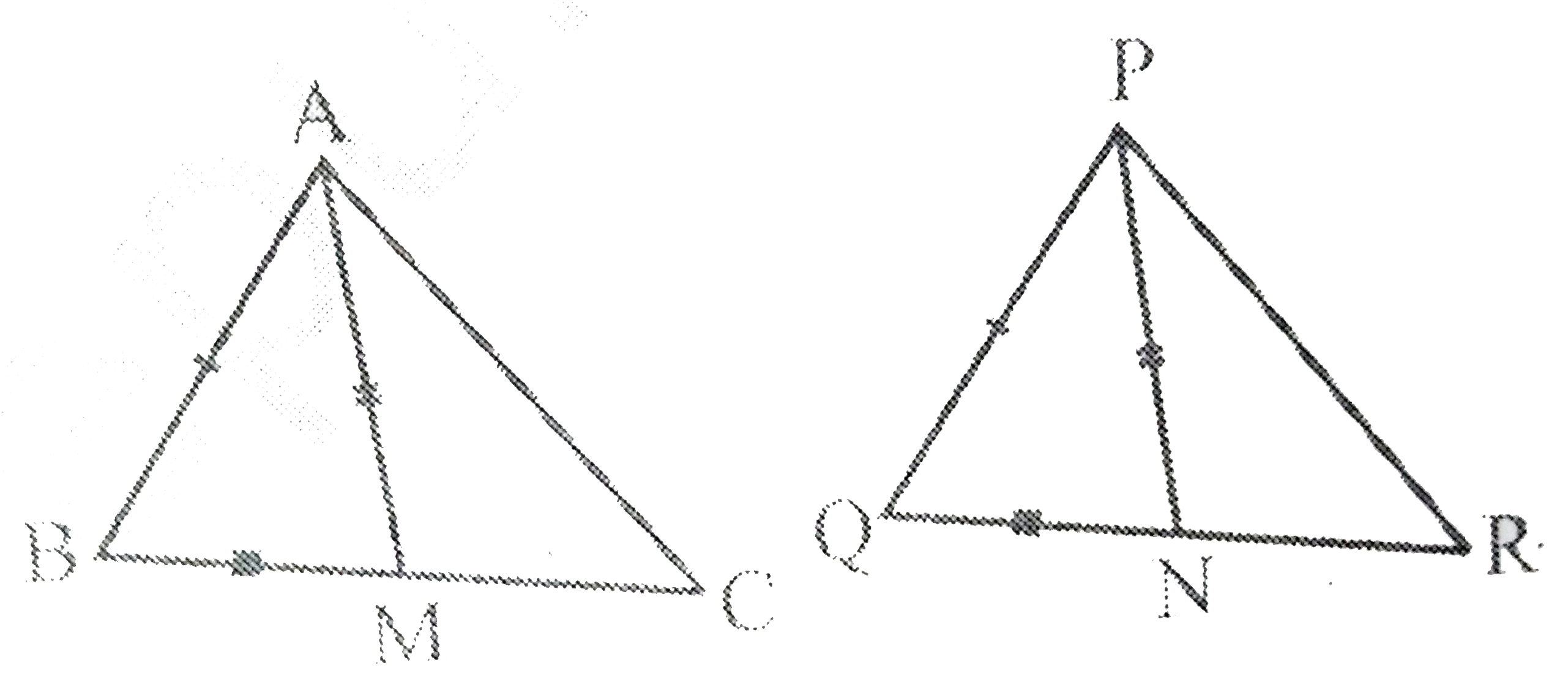
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to side PQ and QR and median PN of ΔABC≅ΔPQR(see Fig. 7.40). Show that:
(i) ΔABM≅ΔPQN
(ii) ΔABC≅ΔPQR
 View Solution
View SolutionIn figure ABC and AMP are two right triangles, right angles at B and M respectively. Prove that(i) ΔABC~ΔAMP (ii) CAPA=BCMP
 View Solution
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show thatar (APB) × ar (CPD) = ar (APD) × ar (BPC).
View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ. Show that:
(i) ΔAPD≅ΔCQB
(ii) AP=CQ
(iii) ΔABC
(iv) AQ=CP
(v) APCQ is a parallelogram.
 View Solution
View SolutionΔABCand ΔDBCare two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC
 View Solution
View Solution

