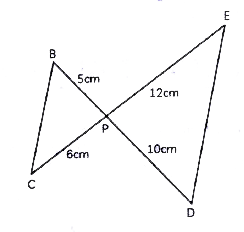
In figure BD and CE intersect each other at the point P. IsΔPBC~ΔPDE? Why?

True.
we have PBPD=510=12 …(1)
and PCPE=612=12 …(2)
PBPD=PCPE [ from (1) and (2) ] …(3)
Now in △PBCand△PDE
∠BPC=∠DPE ( vertically opposite angles)
and PBPD=PCPE
△PBC~△PDE (SAS similarity)

Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6a
23 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Eercise 6b
1 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Revision Exercise Long Questions
4 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
Knowledge Check
In figure, two line segments AC and BD intersects each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD=5 cm, ∠APB=50∘ and ∠CDP=30∘. Then, ∠PBA is equal to
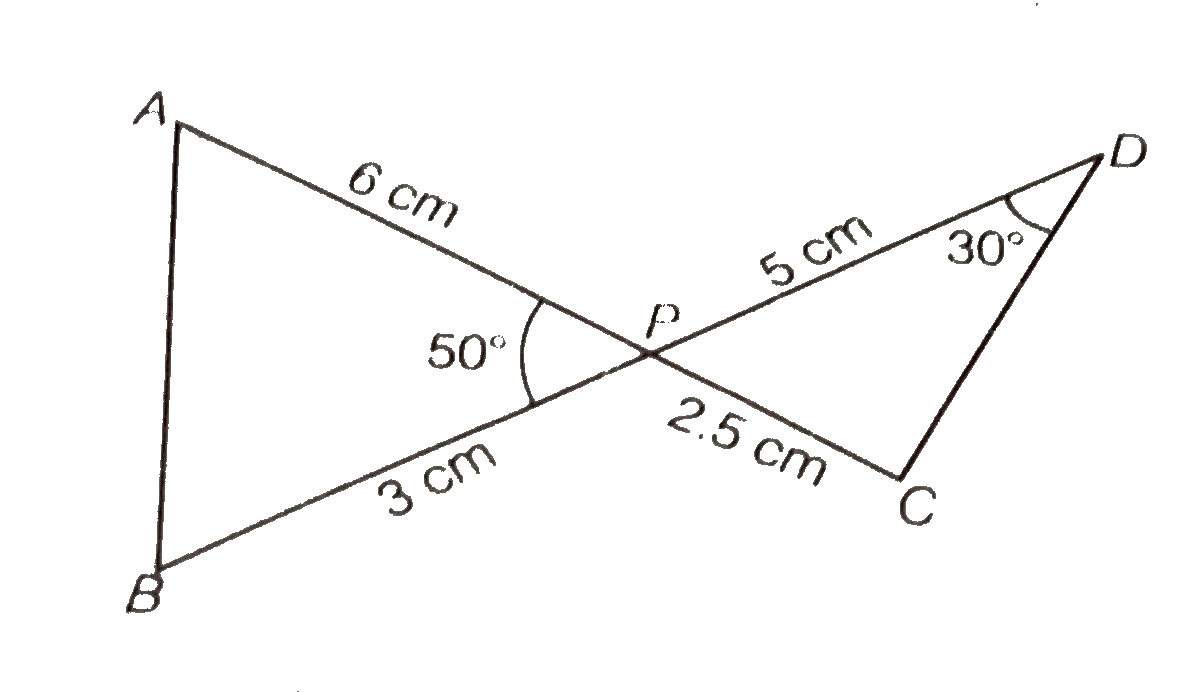 A50∘B30∘C60∘D100∘
A50∘B30∘C60∘D100∘
In the figure, two chords AB and CD intersect each other at the point P.
Prove that : AP. PB = CP. DP

View SolutionIn Figure, two chords AB and CD intersect each other at the point P. Prove that:
(i) ΔAPC~ΔDPB
(ii) AP⋅PB=CP⋅DP

View SolutionIn figure , if AB||DC and AC, PQ intersect each other at the point O. Prove that OA.CQ=OC.AP.

View SolutionIn the figure given below altiudes AD and CE of ΔABC intersect each other at the point P. Show that .
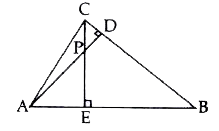
ΔAEP~ΔCDP
View SolutionIn the figure , altitudes AD and CE of ΔABC intersect each other at the point P . Show that :
ΔAEP~ΔCDP
View SolutionIn the figure given below altiudes AD and CE of ΔABC intersect each other at the point P. Show that .
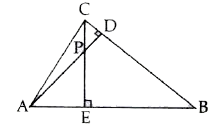
ΔABD~ΔCBE
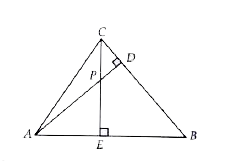
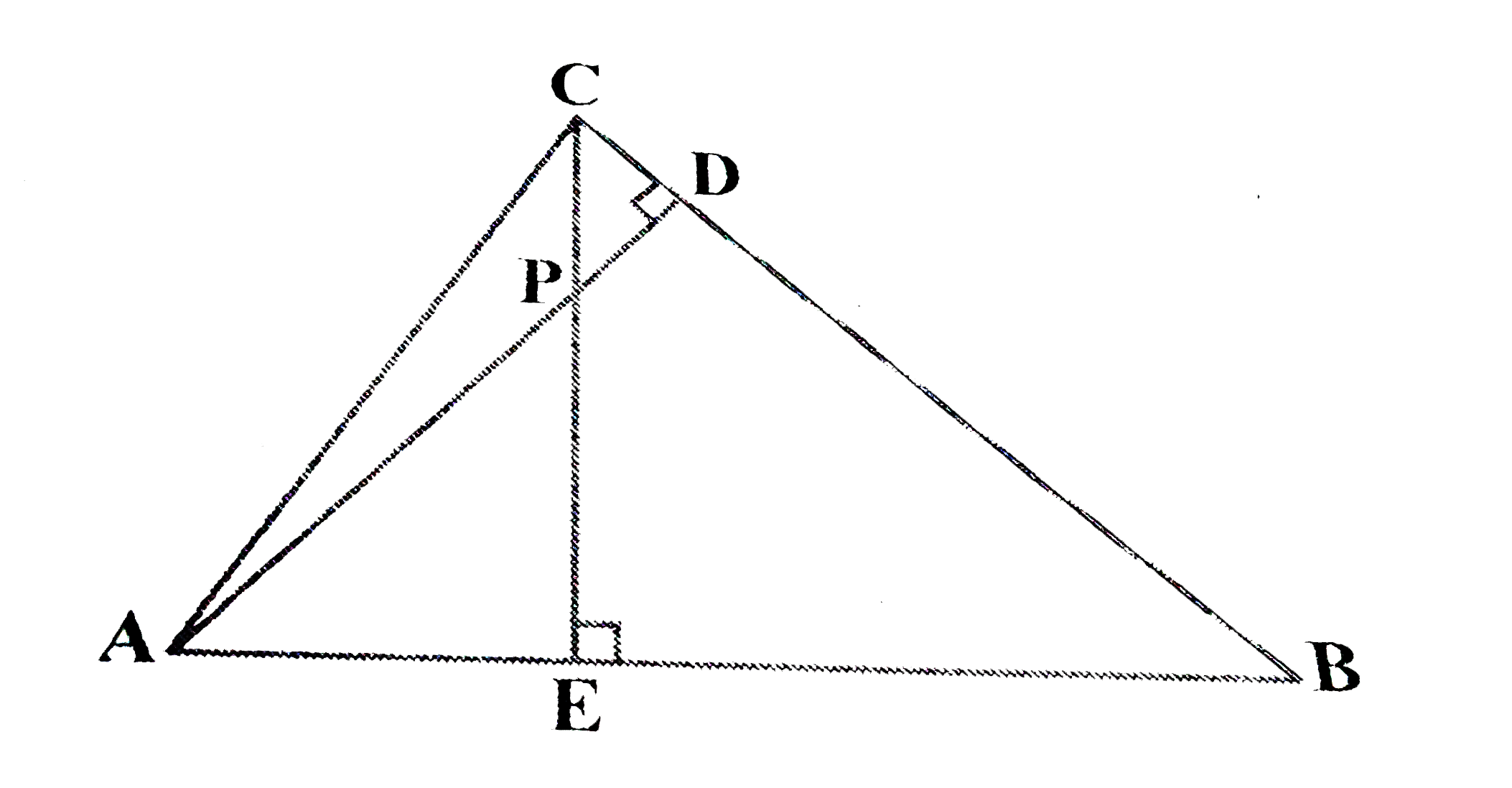
View SolutionIn Figure altitudes AD and CE of DABC intersect each other at the point P. Show that:
(i) ΔAEP~ΔCDP
(ii) ΔABD~ΔCBE
(iii) ΔAEP~ΔADB
(iv) ΔPDC~ΔBEC
View Solution