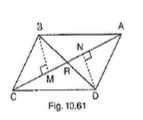
In a ABC, BM and CN are perpendiculars from B and C respectively on any line passing through A. If L is the mid-point of BC , prove that ML=NL .
here in triangles
△BLM and △CLN
∠BML=∠CNL=900
BL=LC (L is a mid point BC).
∠MLB=∠NLC ( vertically opposite angles)
Therefore,
△BLM≅△CLN
Hence,from CPCT we have LM=LN
Topper's Solved these Questions
Similar Questions
BM and CN are perpendicular to a line passing through the vertex A of a triangle ABC. If L is the mid-point of BC , prove that LM=LN
View SolutionBD is one of the diagonals of a quadrilateral ABCD. AM and CN are the perpendiculars from A and C , respectively, on BD. Show That ar (qua..ABCD)=12BD.AM+CN
View SolutionIn a ABC , If LandM are points on ABandAC respectively such that LMparallel BC
Prove that: ar(LOB)=ar(MOC)View SolutionIn a ABC, If LandM are points on ABandAC respectively such that LMparallelBC
Prove that: ar(LCM)=ar(LBM)View SolutionIn a ABC, If LandM are points on ABandAC respectively such that LMparallelBC
Prove that: ar(LBC)=ar(MBC)View SolutionIn a ABC , If LandM are points ABandAC respectively such that LMparallelBC
Prove that: ar(ABM)=ar(ACL)View SolutionIn square ABCD, P and Q are mid-point of AB and CD respectively. If AB=8cm and PQ and BD intersect at O, then find area of OPB
View SolutionIn a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
View SolutionIn ABC , AL and CM are the perpendiculars from the vertices A and C to BC and AB respectively. If AL and CM intersect at O , prove that: (i) OMAOLC (ii) OAOC=OMOL
View SolutionIn Figure, BM and DN are both perpendiculars to the segments AC and BM=DN . Prove that AC bisects BD
 View Solution
View Solution

