BD is one of the diagonals of a quadrilateral ABCD. AM and CN are the perpendiculars from A and C , respectively, on BD. Show That ar (qua..ABCD)=12BD.AM+CN
Given: BD is one of the diagonals of a quadrilateral ABCD. AM and CN are the perpendiculars from
A and C respectively.
To prove: ar(quad.ABCD)=12BD×(AM+CN)
Proof: ar(quad.ABCD)=ar(△ABD)+ar(△BCD)
ar(quad.ABCD)=12(BD×AM)+12(BD×CN)
∴ar(quad.ABCD)=12BD×(AM+CN)
Topper's Solved these Questions
Similar Questions
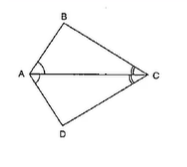
In Figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C . Prove that AB=AD and CB=CD
 View Solution
View SolutionIn a ABC, BM and CN are perpendiculars from B and C respectively on any line passing through A. If L is the mid-point of BC , prove that ML=NL .
View SolutionIn a ABC, If LandM are points on ABandAC respectively such that LMparallelBC
Prove that: ar(LCM)=ar(LBM)View SolutionIn a ABC , If LandM are points on ABandAC respectively such that LMparallel BC
Prove that: ar(LOB)=ar(MOC)View SolutionO is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(OAB)=ar(OBC)
View SolutionIn a ABC, If LandM are points on ABandAC respectively such that LMparallelBC
Prove that: ar(LBC)=ar(MBC)View SolutionIn a cyclic quadrilateral ABCD, if AB ∣∣ CD and ∠B=70∘, find the remaining angles.
View SolutionThe diagonals of quadrilateral ABCD,ACandBD intersect in O. Prove that if BO=OD, the triangles ABCandADC are equal in area.
View SolutionIn Figure, BM and DN are both perpendiculars to the segments AC and BM=DN . Prove that AC bisects BD
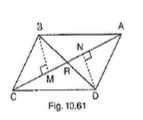 View Solution
View SolutionIn a ABC , If LandM are points ABandAC respectively such that LMparallelBC
Prove that: ar(ABM)=ar(ACL)View Solution

