In $A B C$ , a line $X Y$ parallel to $B C$ cuts $A B$ at $X$ and $A C$ at $Y$ . If $B Y$ bisects $∠ X Y C$ , then $B C = C Y$ (b) $B C = B Y$ (c) $B C \neq C Y$ (d) $B C \neq B Y$

BC =CY

BC =BY

$B C \neq C Y$

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Answer

Step by step video, text & image solution for In A B C , a line X Y parallel to B C cuts A B at X and A C at Y . If B Y bisects /_X Y C , then B C=C Y (b) B C=B Y (c) B C!=C Y (d) B C!=B Y by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Multiple Choice Questions) (LEVEL -2)
15videos
TRIANGLES
BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Match the following )
3videos
TRIANGLES
BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - NCERT Section Exercise 6 .6
12videos
TRIANGLES
BOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - OLYMPIAD/HOTS CORNER
20videos
SURFACE AREAS AND VOLUMES

Knowledge Check

Question 1 - Select One
If $\frac{a + b}{c + d} = \frac{x}{y}$ , then y=_____
A $y = x (a + b) (c + d)$
B $y = \frac{x}{(a + b) (c + d)}$
C $y = \frac{x (c + d)}{a + b}$
D $y = \frac{(a + b)}{c + d}$

$X Y$ isa line parallel to side $B C$ of $A B C . B E A$ and $C F A B$ meet $X Y$ in $E$ and $F$ respectively.Show that $a r (A B E) = a r (A C F) .$
View Solution
$A B C D$ is a parallelogram and line segments $A X, C Y$ bisect the angles $A and C,$ respectively. Show that $A X ∣ ∣ C Y$
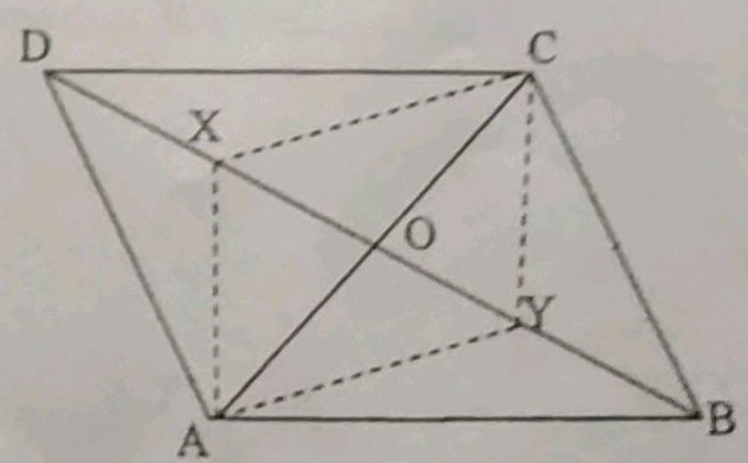
View Solution
In Figure, $A B C D$ is a parallelogram and $X a n d Y$ are points on the diagonal $B D$ such that $D X = B Y$ . Prove that $A X C Y$ is a parallelogram (ii) $A X = C Y, A Y = C X$ $A Y B ≅ C X D$ (iv) $A X D ≅ C Y B$

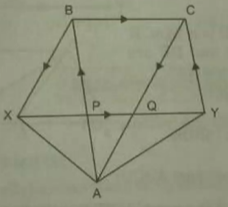
View Solution
$A B C D$ is a trapezium with $A B D C .$ A line parallel to $A C$ intersects $A B$ at $X$ and $B C$ at $Y .$ Prove that $a r (A D X) = a r (A C Y) .$

View Solution
The curves $y = a e^{x}$ and $y = b e^{- x}$ cut orthogonally, if $a = b$ (b) $a = - b$ (c) $a b = 1$ (d) $a b = 2$
View Solution
If $x = b - c + a, y = c - a + b, z = a - b + c$ , then prove that $(b - a) x + (c - b) y + (a - c) z = 0$
View Solution
If the line $y = x$ touches the curve $y = x^{2} + b x + c$ at a point $(1, 1)$ then $b = 1, c = 2$ (b) $b = - 1, c = 1$ (c) $b = 2, c = 1$ (d) $b = - 2, c = 1$
View Solution

MTG IIT JEE FOUNDATION-TRIANGLES - Exercise (Multiple Choice Questions) (LEVEL -1 )

Two isosceles triangles have equal angles and their areas are in the ...
03:03
If A B C and D E F are similar such that 2\ A B=D E and B C=8c m ...
01:16
In A B C , a line X Y parallel to B C cuts A B at X and A C at Y ....
02:34
Let ABC be an equilateral triangel. Let BE|CA meeting CA at E, then (A...
02:45
A right triangle has hypotenuse of length p\ c m and one side of...
01:39
ABC is an isosceles triangle with AC = BC. If A B^2=2A C^2, prove tha...
01:25
DeltaABC is a right triangle , right angled at A and ADbotBC . If AB...
05:03
Delta ABC is right-angled at A and AD bot BC. If BC=13 cm and AC=5 cm,...
03:04
L and M are the mid points of AB and BC respectively of DeltaABC , r...
01:43
In the given figure , x in terms of a , b and c is
02:14
In figure, two line segments AC and BD intersects each other at the po...
03:17
In the given figure , value of x is
02:03
In the given figure , if (AB)/(AC)=(BD)/(CD) , then angleABD=
02:29
The point in the plane of a triangle which is at equal perpendicular d...
02:14
PSR is a triangle right angled at s . D is the mid -point of SR .If t...
Text Solution
An isosceles triangle has a 10 inches base and two 13 inches sides .W...
05:47
If the ratio of the perimeter of two similar triangles is 4:25, then f...
03:29
In DeltaABC,angleB=90^(@)andBDbotAC. If DC=7 cm and AD = 3 cm , then t...
02:36
In which of the following options ,DE ||AB where D and E lie on the si...
04:18
In the given figure , DeltaABC~DeltaPQR ,PM is median of DeltaPQR . I...
03:18

Home
Ask Doubt
Profile

In A B C , a line X Y parallel to B C cuts A B at X and A C at Y . If B Y bisects ∠ X Y C , then B C = C Y (b) B C = B Y (c) B C ≠ C Y (d) B C ≠ B Y

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

If a+bc+d=xy, then y=_____

MTG IIT JEE FOUNDATION-TRIANGLES - Exercise (Multiple Choice Questions) (LEVEL -1 )

In $A B C$ , a line $X Y$ parallel to $B C$ cuts $A B$ at $X$ and $A C$ at $Y$ . If $B Y$ bisects $∠ X Y C$ , then $B C = C Y$ (b) $B C = B Y$ (c) $B C \neq C Y$ (d) $B C \neq B Y$

If $\frac{a + b}{c + d} = \frac{x}{y}$ , then y=_____