In which of the following options ,DE ||AB where D and E lie on the sides AC and BC of ΔABC respectively ?
AD = 6 , EC = 14 , BC = 18 , DC = 21
BE = 20 , Dc = 10 , AC = 25 , BC =36
AC = 10 , Dc = 4 , EC =2 , BC =6
None of these
The correct Answer is:A
To determine in which of the given options DE is parallel to AB in triangle ABC, we will use the properties of similar triangles and the Basic Proportionality Theorem (also known as Thales' theorem). This theorem states that if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
1. Identify the Triangle and Points:
Let triangle ABC be given with points D and E on sides AC and BC respectively.
2. Understand the Condition for Parallel Lines:
According to the Basic Proportionality Theorem, if DE || AB, then:
ADDC=BEECorADAB=BEBC
3. Check Each Option:
- Option A:
- Given: AD=6, EC=14, BC=18
- Calculate EB=BC−EC=18−14=4
- Calculate DC=20
- Check the ratio:
ADDC=620=310
BEEC=414=27
- Since 310≠27, this option does not satisfy the condition.
- Option B:
- Given: BE=20, DC=10, AC=25
- Calculate AD=AC−DC=25−10=15
- Calculate CE=BC−BE=36−20=16
- Check the ratio:
ADDC=1510=32
BEEC=2016=54
- Since 32≠54, this option does not satisfy the condition.
- Option C:
- Given: AC=10, DC=4, CE=2, BC=6
- Calculate AD=AC−DC=10−4=6
- Calculate BE=BC−CE=6−2=4
- Check the ratio:
ADDC=64=32
BEEC=42=2
- Since 32≠2, this option does not satisfy the condition.
4. Conclusion:
After checking all options, only Option A satisfies the condition for DE to be parallel to AB.
Let triangle ABC be given with points D and E on sides AC and BC respectively.
According to the Basic Proportionality Theorem, if DE || AB, then:
ADDC=BEECorADAB=BEBC
- Option A:
- Given: AD=6, EC=14, BC=18
- Calculate EB=BC−EC=18−14=4
- Calculate DC=20
- Check the ratio:
ADDC=620=310
BEEC=414=27
- Since 310≠27, this option does not satisfy the condition.
- Given: BE=20, DC=10, AC=25
- Calculate AD=AC−DC=25−10=15
- Calculate CE=BC−BE=36−20=16
- Check the ratio:
ADDC=1510=32
BEEC=2016=54
- Since 32≠54, this option does not satisfy the condition.
- Given: AC=10, DC=4, CE=2, BC=6
- Calculate AD=AC−DC=10−4=6
- Calculate BE=BC−CE=6−2=4
- Check the ratio:
ADDC=64=32
BEEC=42=2
- Since 32≠2, this option does not satisfy the condition.
After checking all options, only Option A satisfies the condition for DE to be parallel to AB.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Multiple Choice Questions) (LEVEL -2)15videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Match the following )3videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - NCERT Section Exercise 6 .612videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - OLYMPIAD/HOTS CORNER20videos
SURFACE AREAS AND VOLUMES
Similar Questions
CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG show that :
CDGH=ACFGView SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG show that :
ΔDCB~ΔHGEView SolutionIn the adjoning figure, D and E are the points on the sides AB and AC respectively of ΔABC and area of ΔBCE= area of ΔBCD.
Prove that DE∣∣BC
 View Solution
View SolutionIn the adjoining figure D, E and F are the mid - points of the sides BC, AC and AB respectively to triangle. Show that ∠EDF=∠A, ∠DEF=∠B and ∠DFE=∠C:
 View Solution
View SolutionIn the given Fig. 3, in ΔABC,DandE are the mid point of the sides AB and AC respectively. Find the length of DE. Prove that DE=12BC.
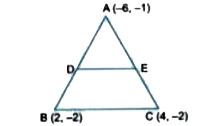 View Solution
View SolutionΔABC is right angle triangle, where ∠B=90∘. D and E lies on sides AB and BC respectively, find the value of AC2+DE2?
View SolutionIn △ ABC, D is the midpoint of BC. DFZAB and DE ⊥ AC, where points F and E lie on AB and AC respectively. If DF = DE, prove that /\ ABC is an isosceles triangle.
View SolutionIn an isosceles triangle ABC with AB=AC, a circle passing through B and C intersects the sides ABandAC atDandE respectively. Prove that DECB.
View SolutionThe incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively . Prove that BD = DC.
 View Solution
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, AC and AB respectively. △DEF is congruent to triangle :
 View Solution
View Solution

