In a ΔABC, AB=15cm, BC=13cm and AC=14cm. Find the area of ΔABC and hence its altitude on AC
Solution
Area of triangle= √s(s−a)(s−b)(s−c)
where s is the semi-perimeter
Here, s=213+14+15=21
Therefore, area= √21(6)(7)(8)=√7056=84units2
Using Area= 21'×base×height:
84=21×14×h⟹h=12cm
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a triangle a = 13 , b = 14, c = 15, r =
A4B8C2D6
In Figure, ABCD is a rectangle with sides AB=10cmandAD=5cm Find the area of EFG

View SolutionIn Figure, ABCD is a rectangle in which CD=6cm,AD=8cm Find the area of parallelogram CDEF

View SolutionAB and CD are two chords of a circle such that AB=6 cm, CD=12 cm and ABCD. If the distance between AB and CD is 3 cm, find the radius of the circle.
View SolutionIn Fig.38, ABCD and PQRC are square such that AD=22 cm and PC=y cm. If the area of the shaded region is 403 cm2, then the value of y is (a)3 (b) 6 (c)9 (d) 10
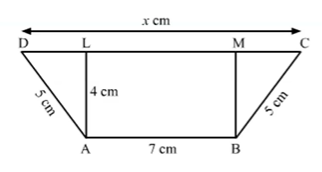
View SolutionIn Figure, ABCD is a trapezium in which AB=7cm, AD=BC=5cm, DC=x cm, and distance between AB and DC is 4cm . Find the value of x and area of trapezium ABCD
View SolutionIn an isosceles triangle ABC , if AB=AC=25cm and BC=14cm , then the measure of altitude from A on BC is (a) 20cm (b) 22cm (c) 18cm (d) 24cm
View SolutionDraw a triangle ABC with AB=6 cm, BC=7 cm and CA=8 cm. Using ruler and compass alone, draw (i) the bisector AD of ∠A and (ii) perpendicular AL from A on BC. Measure LAD.
View Solution