In a ΔABC,BD is the median to the side Ac, BD is produced to E such that BD = DE. Prove that AE is parallel to BC.
To prove that line AE is parallel to line BC in triangle ABC, where BD is the median to side AC and BD is extended to E such that BD = DE, we can follow these steps:
1. Identify the triangle and the median:
- Consider triangle ABC with D as the midpoint of side AC. Therefore, AD = DC.
2. Extend the median:
- Extend line segment BD to point E such that BD = DE. This means that DE is equal in length to BD.
3. Form triangles:
- We will consider triangles ADE and BDC.
4. Identify equal sides:
- From the construction, we know that:
- AD = DC (since D is the midpoint of AC)
- BD = DE (by construction)
5. Identify the angles:
- The angle ADE is equal to angle BDC. This is because they are vertical opposite angles.
6. Use the Side-Angle-Side (SAS) Congruence Criterion:
- We have:
- AD = DC (1st side)
- BD = DE (2nd side)
- Angle ADE = Angle BDC (included angle)
- Therefore, by the SAS criterion, triangle ADE is congruent to triangle BDC.
7. Apply Corresponding Parts of Congruent Triangles (CPCT):
- Since triangles ADE and BDC are congruent, we can say:
- Angle EAD = Angle BCD (by CPCT)
- Angle CBD = Angle AED (by CPCT)
8. Establish parallel lines:
- Since angle EAD is equal to angle BCD and angle CBD is equal to angle AED, we can conclude that:
- AE is parallel to BC (by the Alternate Interior Angles Theorem).
Conclusion:
Thus, we have proved that line AE is parallel to line BC.
---
- Consider triangle ABC with D as the midpoint of side AC. Therefore, AD = DC.
- Extend line segment BD to point E such that BD = DE. This means that DE is equal in length to BD.
- We will consider triangles ADE and BDC.
- From the construction, we know that:
- AD = DC (since D is the midpoint of AC)
- BD = DE (by construction)
- The angle ADE is equal to angle BDC. This is because they are vertical opposite angles.
- We have:
- AD = DC (1st side)
- BD = DE (2nd side)
- Angle ADE = Angle BDC (included angle)
- Therefore, by the SAS criterion, triangle ADE is congruent to triangle BDC.
- Since triangles ADE and BDC are congruent, we can say:
- Angle EAD = Angle BCD (by CPCT)
- Angle CBD = Angle AED (by CPCT)
- Since angle EAD is equal to angle BCD and angle CBD is equal to angle AED, we can conclude that:
- AE is parallel to BC (by the Alternate Interior Angles Theorem).
Thus, we have proved that line AE is parallel to line BC.
Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Exercise 7b
15 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar
5 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHANCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
A point D is taken on the side BC of a ΔABC such that BD=2DC. Prove that ar(ΔABD)=2ar(ΔADC)
View SolutionD is a point on the circumcircle of ΔABC in which AB=AC such that B and D are on the opposite sides of AC. If CD is produced to a point E such that CE=BD. Prove that AD=AE.
View SolutionIn ΔABC, BD and CE are perpendicluars to the sides AC and AB respectively and BD = CE. Prove that ΔBCD≅ΔCBE.
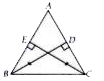
View SolutionIn ΔABC,AB=AC. Side BC is produced to D. Prove that (AD2−AC2)=BD⋅CD.
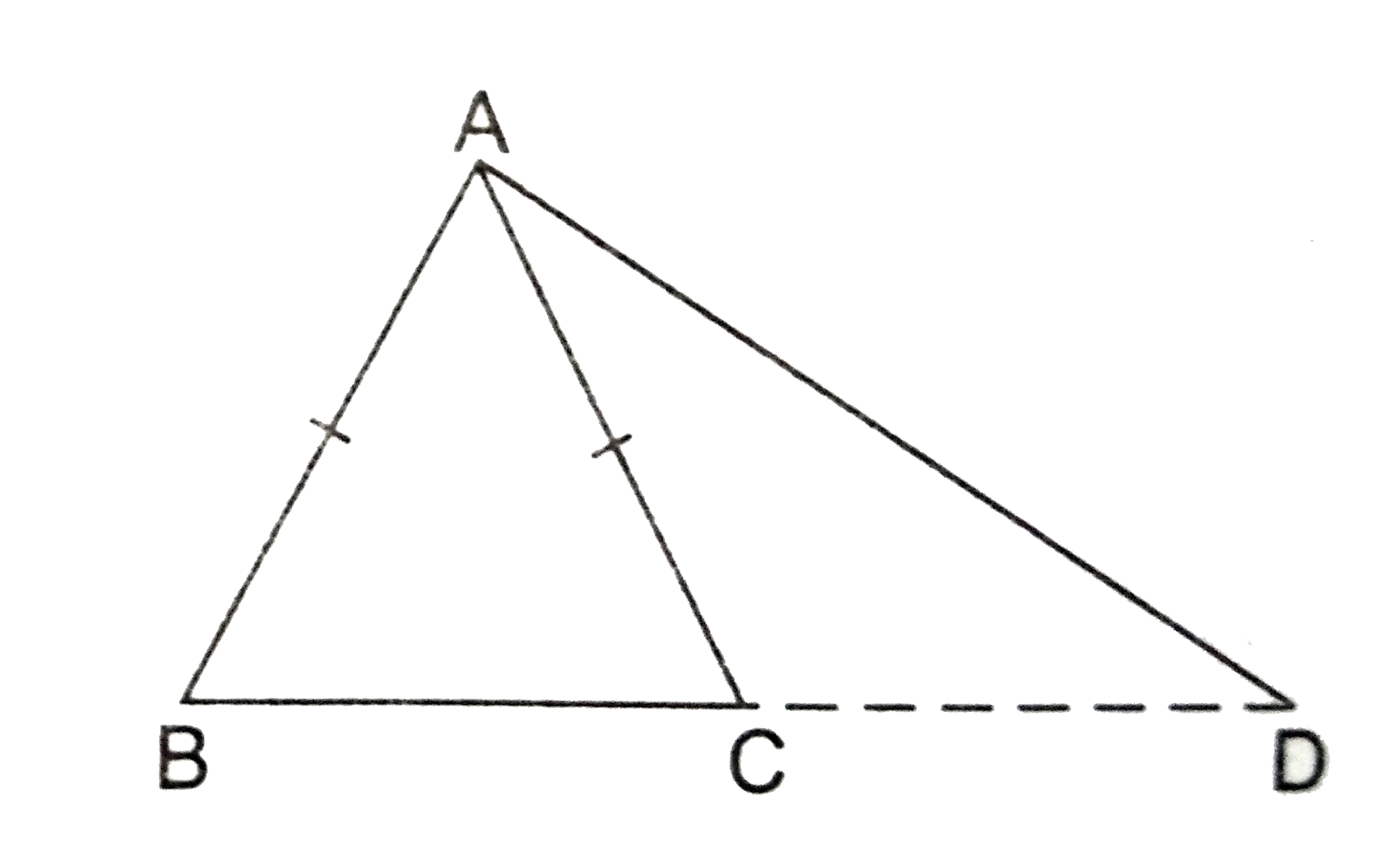
View SolutionIn ΔABC,AB=AC and D is a point in BC so that BD=CD. Prove that AD bisects ∠BAC.
View SolutionD is a point on the circumcircle of ABC in which AB=AC such that B and D are on the opposite side of line AC. If CD is produced to a point E such that CE=BD, prove that AD=AE
View SolutionIn Figure, AD=AE and D and E are points on BC such that BD=EC. Prove that AB=AC
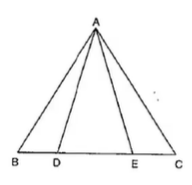
View SolutionIn ΔABC,D is point on side AB and E is a point on side AC such that ∠ADE=∠ABC,AD=2,BD=3 and AE=3, then what is the value of CE ?
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
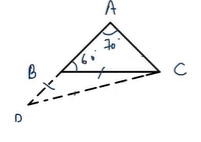
View SolutionIn ABC, side AB is produced to D so that BD=BC. If ∠B=600 and ∠A=700, prove that: AD>CD (ii) AD>AC
View Solution
