In a game of chance, a spining arrow comes to rest at one of the numbers
1,2,3,4,5,6,7,8,
All these are equally likely outcomes.
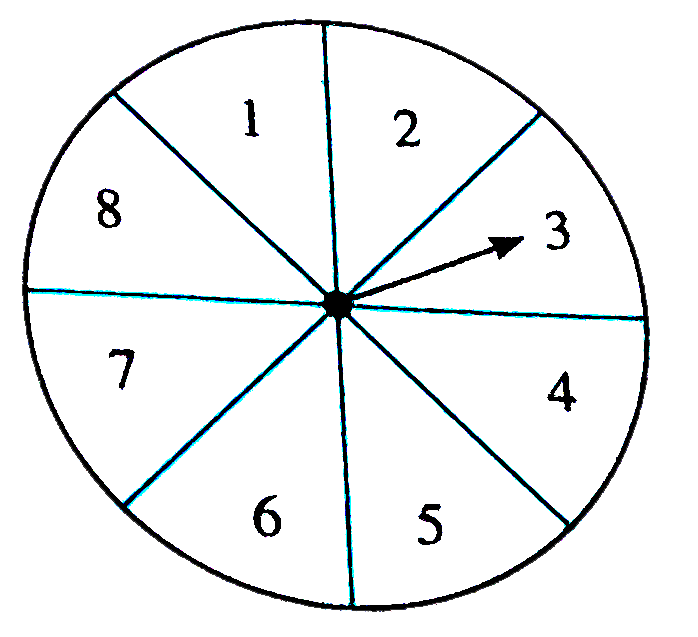
Find the probability that it will rest at
The correct Answer is:(i) P(A)=18, (ii) P(B)=12, (iii) P(C)=34, (iv) P(D)=1
Step by step video & image solution for In a game of chance, a spining arrow comes to rest at one of the numbers 1,2,3,4,5,6,7,8, All these are equally likely outcomes. Find the probability that it will rest at by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROBABILITYBOOK - TARGET PUBLICATIONCHAPTER - PROBABILITYEXERCISE - (Multiple Choice Questions)
8 Videos
- PROBABILITYBOOK - TARGET PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Additional Problems for Practice (Based on Practice Set 5.1)
3 Videos
- PROBABILITYBOOK - TARGET PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Practice Set 5.4
5 Videos
- MODEL QUESTION PAPER (PART - II)BOOK - TARGET PUBLICATIONCHAPTER - MODEL QUESTION PAPER (PART - II)EXERCISE - Questions
28 Videos
- PYTHAGORAS THEOREM BOOK - TARGET PUBLICATIONCHAPTER - PYTHAGORAS THEOREM EXERCISE - Chapter Assessment
16 Videos
Similar Questions
In a game of chance, the spinning arrow rests at one of the numbers 1,2,3,4,5,6,7,8. All these are equally likely outcomes. Find the probability of the following events:
(a) The arrow rests at an odd number.
It rests at a prime number.
It rests at a multiple of 2.
View SolutionIn a game of chance, the spinning arrow rests at one of the numbers 1,2,3,4,5,6,7,8. All these are equally likely outcomes. Find the probability of the following events.
(i) the arrow rests at an odd number
(ii) it rests at a prime number
(iii) it rests at a multiple of 2.
View Solution
Knowledge Check
A game of chance consists of spinning an arrow, which comes to rest pointing at one of the numbers 1,2,3,4,5,6,7,8 and these are equally likely outcomes. Find the probability that the arrow will point at any factor of 8.
A58B78C18D38
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1,2 3,4,5,6,7,8 and these are equally likely outcomes what is the probability that it will point at :
(i) 8?
(ii) an odd number ?
(iii) a number greater than 2 ?
(iv) a number less than 9 ?
View SolutionA game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1,2,3,4,5,6,1,8 (see Figure), and these are equally likely outcomes. What is the probability that it will point at(i) 8?(ii) an odd number?(iii) a number greater than 2?(iv) a number less than 9?
View SolutionA game of chance consist of spinning an arrow which comes to rest pointing at one of the numbers 15,20,25,30,35,40,45,50 and these are equally likely outcomes. What is the probability that it will point at
(i) an even number? (ii) at a number multiple of 5
(iii) at a number divisible by 3 (iv) at a prime number.
View SolutionA game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (See Fig. 131), and these are equally likely outcomes. What is the probability that it will point at (i) 8? (ii) an odd number? (iii) a number greater than 2? (iv) a number less than 9?
View SolutionA game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (see figure) and these are equally likely outcomes. What is the probability that it will point at :
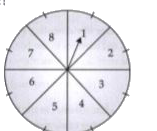
(i) 8? (ii) an odd number?
(iii) a number greater than 2? (iv) a number less 9?
View SolutionRead the following text and answer the following question on the basis of the same.
A game of chances consisting of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (see the figure) and these are equally likely outcomes.
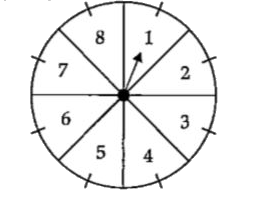
Find the probability that point lie on the number 8.
View SolutionRead the following text and answer the following question on the basis of the same.
A game of chances consisting of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (see the figure) and these are equally likely outcomes.
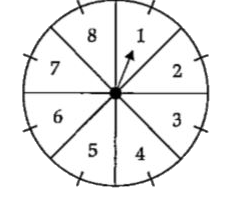
Find out the probability that the pointer is always less than 9.
View Solution
