In a parallelogram ABCD diagonals AC and BD intersect at O and AC=6.8cm and BD=13.6cm. Find the measures of OC and OD.
To find the measures of OC and OD in the parallelogram ABCD, where the diagonals AC and BD intersect at point O, we can follow these steps:
1. Understand the Properties of Parallelograms:
In a parallelogram, the diagonals bisect each other. This means that the point where they intersect divides each diagonal into two equal parts.
2. Identify the Lengths of the Diagonals:
We are given:
- Length of diagonal AC=6.8cm
- Length of diagonal BD=13.6cm
3. Calculate OC:
Since O is the midpoint of diagonal AC:
OC=AC2=6.8cm2=3.4cm
4. Calculate OD:
Similarly, since O is also the midpoint of diagonal BD:
OD=BD2=13.6cm2=6.8cm
Final Results:
- OC=3.4cm
- OD=6.8cm
In a parallelogram, the diagonals bisect each other. This means that the point where they intersect divides each diagonal into two equal parts.
We are given:
- Length of diagonal AC=6.8cm
- Length of diagonal BD=13.6cm
Since O is the midpoint of diagonal AC:
OC=AC2=6.8cm2=3.4cm
Similarly, since O is also the midpoint of diagonal BD:
OD=BD2=13.6cm2=6.8cm
- OC=3.4cm
- OD=6.8cm
Topper's Solved these Questions
Similar Questions
In a parallelogram ABCD diagonals AC and BD intersect at O and AC=6.8 cm and BD=5.6cm . Find the measures of OC and OD
View SolutionABCD is a parallelogram whose diagonals AC and BD intersect at O. A Line through O intersects AB at P and DC at Q. Prove that ar(△POA)=ar(△QOC).
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area. GIVEN : A parallelogram ABCD . The diagonals AC and BD intersect at O. TO PROVE : ar(OAB)=ar(OBC)=ar(OCD)=ar(AOD)
View SolutionIn Figure, ∠AOB=900, AC=BC, OA=12 cm and OC=6.5cm. Find the area of AOB.
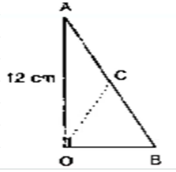 View Solution
View SolutionIn a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB=75∘, then write the value of ∠C+ ∠D
View SolutionIf the diagonals AC,BD of a quadrilateral ABCD, intersect at O, and seqarate the quadrilateral into four triangles of equal area, show that quadrilateral ABCD is a parallelogram. GIVEN : A quadrilateral ABCD such that its diagonals AC and BD intersect at O and separate it into four parts such that ar(AOB)=ar(BOC)=ar(COD)=ar(AOD) TO PROVE : Quadrilateral ABCD is a parallelogram.
View SolutionABCD is a trapezium in which ABCD . The diagonals AC and BD intersect at O . Prove that (i) AOBCOD (ii) If OA=6cm , OC=8cm , Find: Area (AOB)Area (COD) (b) Area (AOD)Area (COD)
View SolutionIn a parallelogram ABCD, AB=10cm, AD=6cm. The bisector of ∠A meets DC in E, AE and BC produced meet at F. Find the length C Foot
View SolutionIn Figure, ABCD is a quadrilateral in which diagonal AC=84 cm ; DL⊥AC, BM⊥AC, DL=16.5 cm and BM=12 cm . Find the area of quadrilateral ABCD.
View SolutionIn Figure, ABCD is a parallelogram, AE ⊥DC and CF⊥AD . If AB=16CM, AE=8cm and CF=10cm, find AD
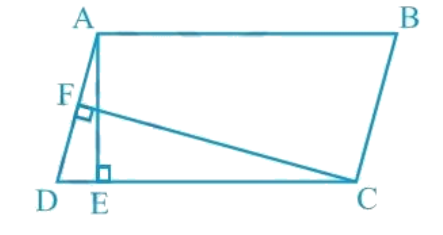 View Solution
View Solution

