In a parallelogram ABCD, the bisector of ∠A also bisects BC at X. prove that AD=2AB.
Given: In parallelogram ABCD, bisector of ∠A bisects BC at X.
To Prove: AD=2AB
Proof: AD parallel to BC and AX cuts them
⇒∠DAX=∠AXB (alternate angles)
∠DAX=∠XAB (AX is bisector of ∠A)
∴∠AXB=∠XAB
AB=BX (sides opposite of equal angles)
Now,
ABAD=BXBC
⇒ABAD=BX2BX (X is mid-point of BC)
⇒ABAD=12
∴AD=2AB
Hence proved.
Topper's Solved these Questions
Similar Questions
In a parallelogram ABCD, the bisector of ∠A also bisects BC at X Find AB:AD
View SolutionIn a parallelogram ABCD, the bisector of ∠A also bisects BC at X. prove that AD=2AB.
View SolutionIn a parallelogram ABCD, if ∠D=115∘, then write the measure of ∠A
View SolutionIn ABC,∠B=2∠C and the bisector of ∠B intersects AC at D. Prove that BDDA=BCBA
View SolutionIn Figure, ABCD is a parallelogram in which ∠A=600 . If the bisectors of ∠A and ∠B meet at P, prove that AD=DP,PC=BC and DC=2AD.
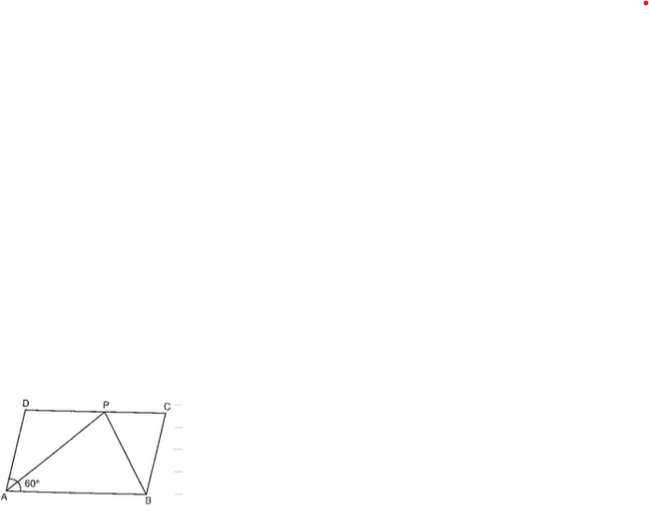 View Solution
View SolutionIn parallelogram ABCD, the angle bisector of ∠A bisects BC. Will angle bisector of B also bisect AD? Give reason.
View SolutionIn a parallelogram ABCD, AB=10cm, AD=6cm. The bisector of ∠A meets DC in E, AE and BC produced meet at F. Find the length C Foot
View SolutionIn a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC=300, ∠BDC=100and ∠CAB=700, Find: ∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB
Given that
∠ABC=302,∠ABC=∠ADC=300
[We know that measure of opposite angles are equal in a parallelogram]
∠BDC=100
∠CAB=700
∠BDA=∠ADB=∠ADC–∠BDC
302–102=202
∠DAB=1800–300=1500
∠ADB=∠DBC=200 (alternate angles)
∠BCD=∠DAB=1500
[we know, opposite angles are equal in a parallelogram]
∠DBA=∠BDC=100
[we know, Alternate interior angles are equal]
InΔABC
∠CAB+∠ABC+∠BCA=1800
[since, sum of all angles of a triangle is 180^0]
700+300+∠BCA=1800
∠BCA=1800–1000=800
∠DAB=∠DAC+∠CAB=700+800=1500
∠BCD=1500 (opposite angle of the parallelogram)
∠DCA=∠CAB=700
In ΔDOC∠BDC+∠ACD+∠DOC=1800
[since, sum of all angles of a triangle is 180^0]
100+700+∠DOC=1800
∠DOC=1800−800
∠ACB=800View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
View SolutionIn a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB=75∘, then write the value of ∠C+ ∠D
View Solution

