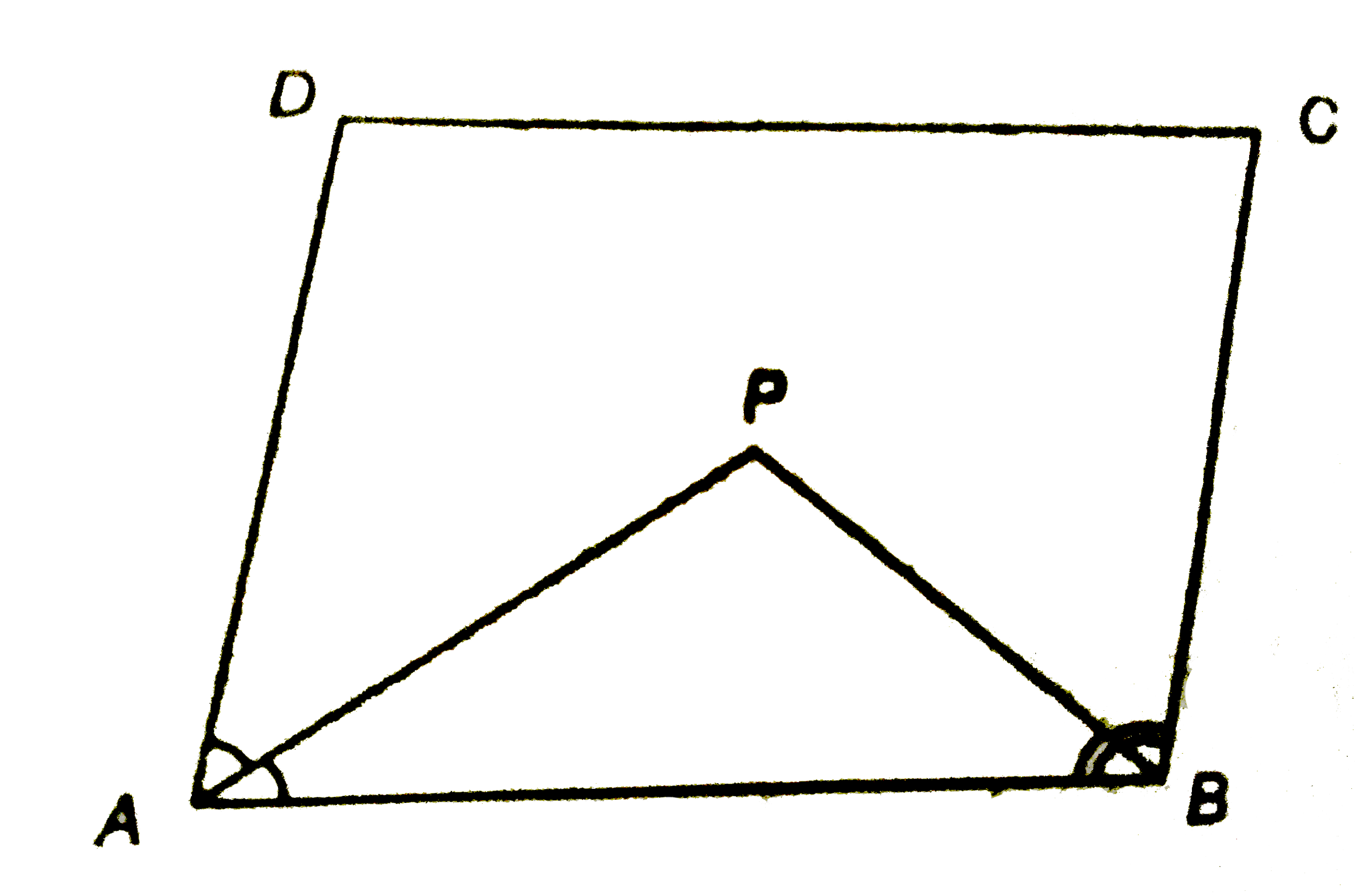
In a parallelogram ABCD, the bisectors of ∠Aand∠B intersect each other at point P. Prove that ∠APB=90∘.
AP is the bisector of ∠A.
∴ ∠DAB=2∠PAB ...(1)
similarly, ∠CBA=2∠PBA ...(2)
We know that
∠CBA+∠CBA=180∘ (sum of co-interior angles of a parallelogram is180∘)
⇒ ∠PAB+∠PBA=90∘ [from(1)and(2)]
In∠APB, ...(3)
∠PAB+∠PBA+∠APB=180∘
⇒ 90∘+∠APB=180∘
⇒ ∠APB=180∘−90∘ (anglesumpoperty)
⇒ ∠APB=90∘ [from(3)]
Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar
11 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a
29 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise
12 Videos
Similar Questions
In parallelogram ABCD, the bisectors of adjacent angles A and D intersect each other at point P. prove that ∠APD=90∘.
View SolutionIn ΔABC, bisectors of ∠Band∠C interesct each other at point O. Prove that ∠BOC=90∘+12∠Ai.e.,∠1=90∘+12A
View SolutionIn ΔABC, bisectors of ∠Band∠C interesct each other at point O. Prove that ∠BOC=90∘+12∠Ai.e.,∠1=90∘+12
View SolutionIn a parallelogram ABCD, the bisector of ∠A bisects the line B at point X. Prove that AD = 2AB.
View SolutionIn a parallelogram ABCD, AX and CY are the bisectors of ∠Aand∠C respectively. Prove that AX||CY.
View SolutionIn triangle LMN, bisector of interior angles at L and N intersect each other at point A. Prove that :
AM bisects angle LMN.
View SolutionIn parallelogram ABCD, P is mid-point of AB. CP and BD intersect each other at point O. If area of ΔPOB=40cm2 and OP:OC= 1:2, find :
(i) Areas of ΔBOC and ΔPBC
(ii) Areas of ΔABC and parallelogram ABCD.
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
ΔAPB is similar to ΔCPD.
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
PA×PD=PB×PC.
View SolutionIn triangle ABC,the bisector of interior angle A and the bisector angle C meet at point O. Prove that ∠AOC=12∠B
View Solution
