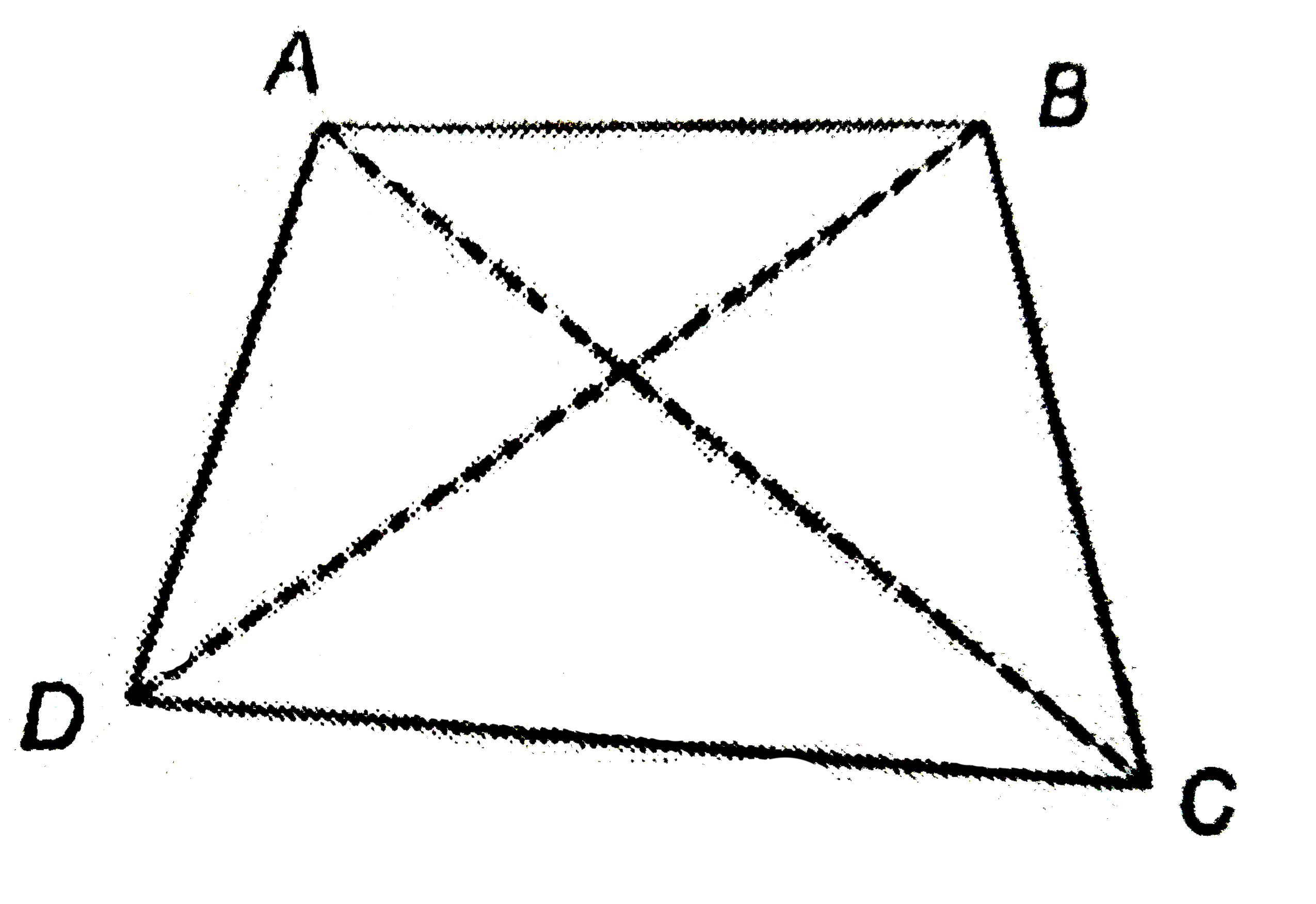
In a quadrilateral ABCD, AB is the shortest side and DC is the longest side. What is the relation between
(i) $∠ B$ and $∠ D$ (ii) $∠ A$ and $∠ C$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:(i) $∠ B > ∠ D$ (ii) $∠ A > ∠ (C)$

Answer

Step by step video, text & image solution for In a quadrilateral ABCD, AB is the shortest side and DC is the longest side. What is the relation between (i) angleB and angleD (ii) angleA and angleC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.

Updated on:21/07/2023

Class 9 MATHS TRIANGLES

Topper's Solved these Questions

Knowledge Check

In a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then
A $A B^{2} + B C^{2} = C D^{2} + D A^{2}$
B $A B^{2} + C D^{2} = B C^{2} + D A^{2}$
C $A B^{2} + A D^{2} = B C^{2} + C D^{2}$
D $A B^{2} + B C^{2} = 2 (C D^{2} + D A^{2})$
In a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then
A $A B^{2} + B C^{2} = C D^{2} + D A^{2}$
B $A B^{2} + C D^{2} = B C^{2} + D A^{2}$
C $A B^{2} + A D^{2} = B C^{2} + C D^{2}$
D $A B^{2} + B C^{2} = 2 (C D^{2} + D A^{2})$
In a $∠ A B C$ , $∠ A$ : $∠ B$ : $∠ C$ = 2 : 4 : 3. The shortest side and the longest side of the triangle are respectively
AAC and AB
BAC and BC
CBC and AC
DAB and AC

NAGEEN PRAKASHAN-TRIANGLES-Revision Exercise (very Short Answer Questions)

Home
Ask Doubt
Profile

In a quadrilateral ABCD, AB is the shortest side and DC is the longest side. What is the relation between (i) ∠B and ∠D (ii) ∠A and ∠C.

The correct Answer is:(i) ∠B>∠D (ii) ∠A>∠(C)

Topper's Solved these Questions

Similar Questions

Knowledge Check

In a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then

In a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then

In a ∠ABC, ∠A : ∠B : ∠C = 2 : 4 : 3. The shortest side and the longest side of the triangle are respectively

NAGEEN PRAKASHAN-TRIANGLES-Revision Exercise (very Short Answer Questions)

In a quadrilateral ABCD, AB is the shortest side and DC is the longest side. What is the relation between
(i) $∠ B$ and $∠ D$ (ii) $∠ A$ and $∠ C$ .

The correct Answer is:(i) $∠ B > ∠ D$ (ii) $∠ A > ∠ (C)$

In a $∠ A B C$ , $∠ A$ : $∠ B$ : $∠ C$ = 2 : 4 : 3. The shortest side and the longest side of the triangle are respectively