In a quadrilateral ABCD angle bisector of ∠Band∠D are meeting at point P and Q respectively on extended sides of CD and AB. Then how ∠Pand∠Q,∠ABCand∠aADC are related.
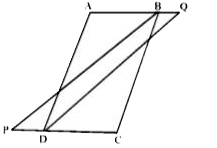
∠P+∠Q=1/2(∠ABC+∠ADC)
∠P+∠Q=(∠ABC+∠ADC)
(∠P+∠Q)=2(∠ABC+∠ADC)
(∠P+∠Q)=(∠ABC+∠ADC)
Step by step video & image solution for In a quadrilateral ABCD angle bisector of angleB and angleD are meeting at point P and Q respectively on extended sides of CD and AB. Then how angleP and angleQ, angleABC and angleaADC are related. by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
In a quadrilateral ABCD, AO and BO are the bisectors of ∠Aand∠B respectively, ∠C=70∘and∠D=30∘. Then, ∠AOB=?
A50∘B130∘C80∘D100∘In a quadrilateral ABCD, ∠D=60∘and∠C=100∘ . The bisectors of ∠Aand∠B meet at the point P. The measure of ∠APB is
A80∘B100∘C60∘D70∘In a quadrilateral ABCD,∠D=60∘and∠C=100∘. The bisectors of ∠Aand∠B meet at the point P. The measure of ∠APB is
A80∘B70∘C100∘D60∘
In a quadrilateral ABCD the linesegment bisecting ∠Cand∠D meet at E. Prove that ∠A+∠B=2∠CED.
View SolutionIn the adjoining figure, AB>AC and the angle bisectors of ∠B and ∠C meet at point P. Prove that
PB>PC.

View SolutionIn a quadrilateral ABCD, AO and BO are the bisectors of ∠Aand∠B respectively. Prove that ∠AOB=12(∠C+∠D).
View SolutionIn a quadrilateral ABCD, the bisectors of ∠C and ∠D meet at E. If ∠CED=56∘ and ∠A=49∘, then the measure of ∠B is:
View SolutionABCD is a parallelogram. If the bisectors of the angle A and angle C meet the diagonal BD at points P and Q respectively, then which one of the following is correct ?
View Solution
