In a quadrilateral ABCD,CO and DO are the bisectors of ∠C and ∠D respectively. Prove that ∠COD=12(∠A+∠B).
In a quadrilateral ABCD,CO
and DO are the bisectors of ∠C and ∠D
respectively
from angle sum A+B+C+D=360∘
A+B+2(∠1+∠2)=360∘
A+B+2(360∘−∠COD)=360∘
we get
∠COD=12(∠A+∠B)
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In a quadrilateral ABCD, AO and BO are the bisectors of ∠Aand∠B respectively, ∠C=70∘and∠D=30∘. Then, ∠AOB=?
A50∘B130∘C80∘D100∘
In a quadrilateral ABCD, AO and BO are the bisectors of ∠Aand∠B respectively. Prove that ∠AOB=12(∠C+∠D).
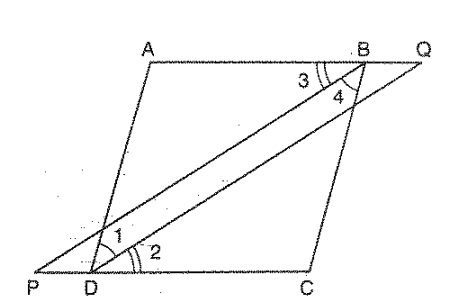
View SolutionIn the figure bisector of ∠B & ∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that ∠P+∠Q=12(∠ABC+∠ADC).
View SolutionIn Figure, bisectors of ∠B and ∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that ∠P+∠Q=12(∠ABC+∠ADC).
 View Solution
View SolutionIn the figure bisector of ∠B & ∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that
∠P+∠Q=12(∠ABC+∠ADC).View SolutionIn Figure, bisectors of ∠B and ∠D of quadrilateral ABCD meet CD and AB produced at Pand Q respectively. Prove that : ∠P+∠Q=12(∠ABC+∠ADC)
View SolutionIn a quadrilateral ABCD, cosAcosB+sinCsinD=
View SolutionABCD is a quadrilateral. The bisectors of angle A and B intersect at P, show that ∠C+∠D=2∠APB.
View Solution

