In Figure, find the
four angles A, B, C and D
in the parallelogram ABCD

Step by step video & image solution for In Figure, find the four angles A ,\ B ,\ C\ a n d\ D in the parallelogram A B C D by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Figure, ABCD, ABFE and CDEF are parallelograms. Prove that ar(ADE)=ar(BCF)
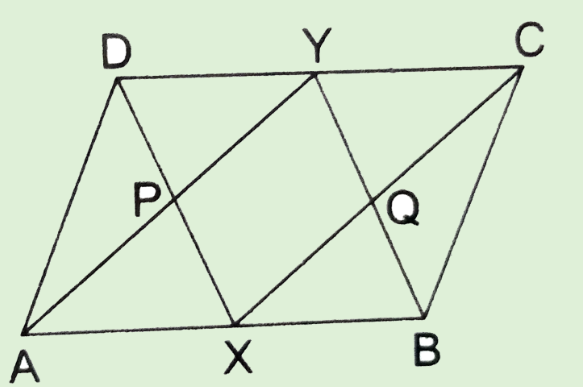
View SolutionIn Figure, X, Y are the mid-points of opposite sides AB and DC of a parallelogram ABCD.AY and DX are joined intersecting in P;CX and BY are joined intersecting in Q . Show that AXCY is a parallelogram (ii) DXBY is a parallelogram quadrilateral PXQY is a parallelogram
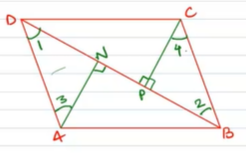
View SolutionIn Figure, AN and CP are perpendicular to the diagonal BD of a parallelogram ABCD. Prove that : ADN≅CBP (ii) AN=CP
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area. GIVEN : A parallelogram ABCD . The diagonals AC and BD intersect at O. TO PROVE : ar(OAB)=ar(OBC)=ar(OCD)=ar(AOD)
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ

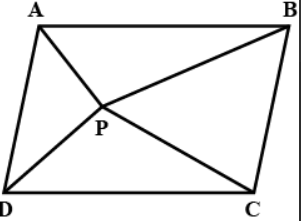
View SolutionABCD IS A PARALLELOGRAM AND O is any point in its interior. Prove that: ar (AOB)+ ar (COD)= ar (BOC)+ ar(AOD) ar (AOB)+ar (COD)=12 ar(^(gm)ABCD) Given: A parallelogram ABCD and O is a point in its interior. To Prove: ar ( AOB)+ ar(COD)=ar (BOC)+ar(AOD)
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
View SolutionA diagonal of a parallelogram divides it into two triangles of equal area. GIVEN : A parallelogram ABCD in which BD is one of the diagonals. TO PROVE : ar (ABD)=ar(CDB)
View SolutionIn Figure, ABCD and AEFG are two parallelograms. If ∠C=580, find ∠F
View Solution
