In a square ABCD, A is joined to a point X on BC and D is joined to a point Y on AB. If AX = DY, prove that AX is perpendicular to DY.
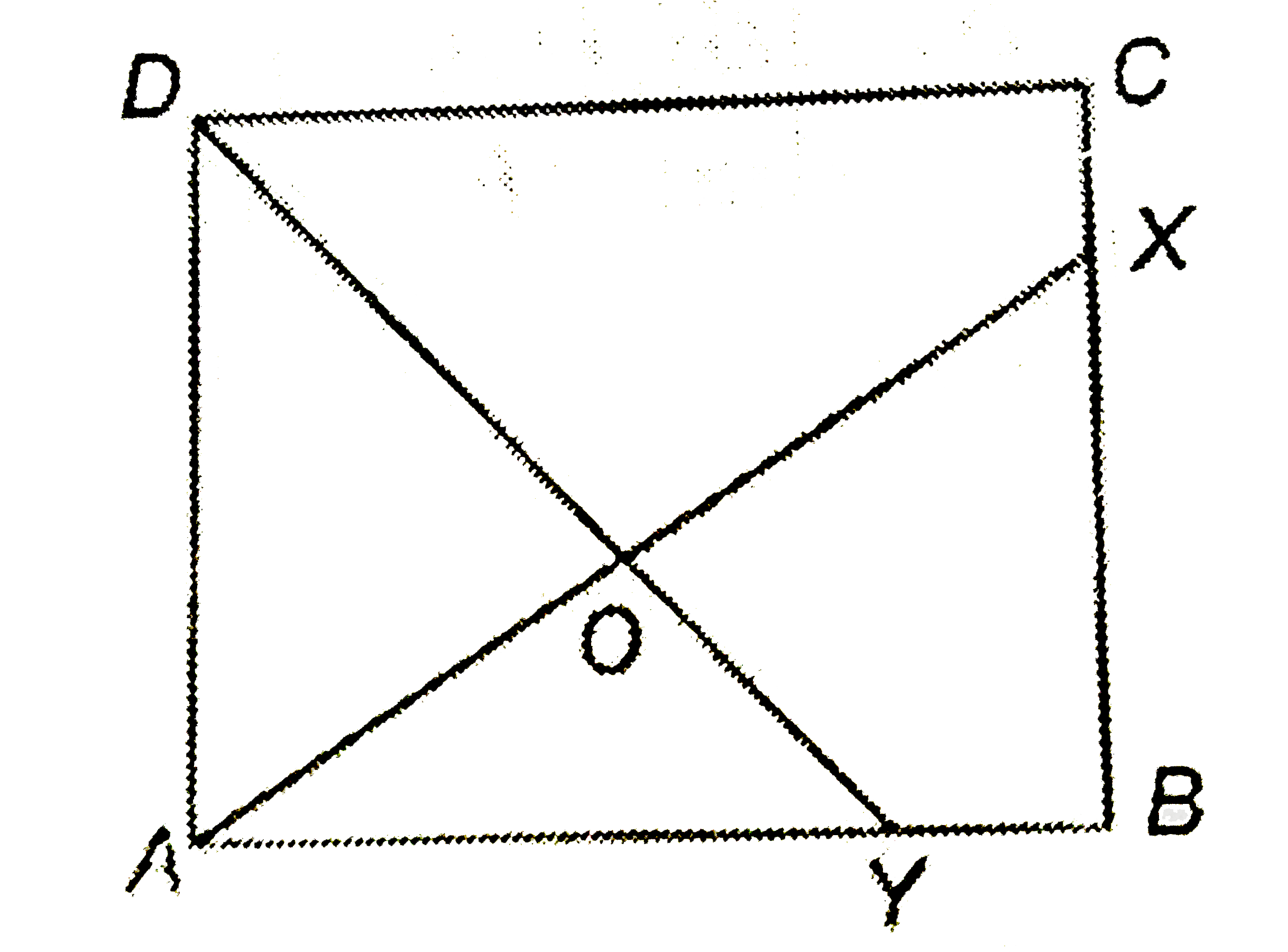
Step by step video, text & image solution for In a square ABCD, A is joined to a point X on BC and D is joined to a point Y on AB. If AX = DY, prove that AX is perpendicular to DY. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (short Answer Questions )
10 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise
10 Videos
Similar Questions
The side BC of a triangle ABC is bisected at D;o is any point in AD,BOandCO produced meet ACandAB in EandF respectively and AD is produced to X so that D is the mid-point of OX. Prove that AO:AX=AF:AB and show that FEBC.
View Solution□ABCD is a parallelogram point E is on side BC. Line DE intersects ray AB in point T. Prove that DE×BE=CE×TE.

View Solution
Knowledge Check
In a square ABCD, A is joined to a point X on BC and D is joined to a point Y on AB. If AX = DY, prove that AX is perpendicular to DY.
 A60∘B120∘C90∘Dcan't be determined
A60∘B120∘C90∘Dcan't be determinedABCD is a square, A is joined to a point P on BC and D is joined to a point Q on AB. If AP=DQ and AP intersects DQ at R the, ∠DRP is :
A60∘B120∘C90∘Dcan't be determinedIf ABCD is a square, X is the mid point of AB and Y is the mid point of BC, then which of the following is NOT correct?
AThe triangles ADX and BAY are congruentB∠DXA=∠AYBC∠ADX=∠BAYDDX is not perpendicular to AY
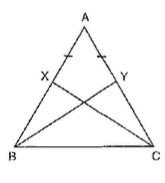
In Figure, X and Y are two points on equal sides AB and AC of a ABC such that AX=AY. Prove that XC=YB.
View SolutionIn Figure, X, Y are two points on equal sides AB and AC of a ABC such that AX=AY. Prove that XC=YB
View SolutionIn parallelogram ABCD, X and Y are mid-points of opposite sides AB and DC respectively. Prove that: (i)AX=YC (ii) AX is parallel to YC (iii)AXCY is parallelogram
View SolutionLet ABCD be a square. An arc of a circle with A as centre and AB as radius is drawn inside the square joining the points B and D. Points P on AB, S on AD, Q and R on arc BD are taken such that PQRS is a square. Further suppose that PQ and RS are parallel toAC. Then, areaPQRSareaABCD is
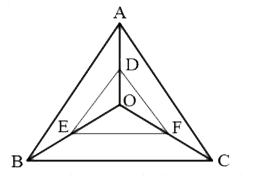
View SolutionIn the figure, a point O inside △ABC is joined to its vertices. From a point D on AO, DE is drawn parallel to AB and from a point E on BO, EF is drawn parallel to BC. Prove that DF || AC.
View Solution
