In the figure, a point O inside $△ A B C$ is joined to its vertices. From a point D on AO, DE is drawn parallel to AB and from a point E on BO, EF is drawn parallel to BC. Prove that DF || AC.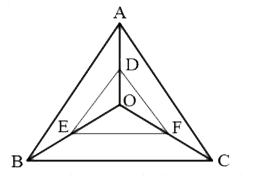

Video Solution

Answer

Step by step video & image solution for In the figure, a point O inside triangleABC is joined to its vertices. From a point D on AO, DE is drawn parallel to AB and from a point E on BO, EF is drawn parallel to BC. Prove that DF || AC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

TRIANGLEBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLEEXERCISE - Short Answer Type Questions-I
10 Videos
SURFACE AREA AND VOLUME BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SURFACE AREA AND VOLUME EXERCISE - PRACTICE TEST ( SECTION-D)
1 Videos

Knowledge Check

In $Δ P Q R$ , QR=10, RP=11 and PQ=12. D is the midpoint of PR, DE is drawn parallel to PQ meeting QR in E. EF is drawn parallel to RP meeting PQ in F. What is the length of DF?
A $\frac{11}{2}$
B6
C $\frac{33}{4}$
D5

In the figure ABCD is a trapezium in which side AB is parallel to side DC and E is the midpoint of side AD. If F is a point on the side BC such that the line segment EF is parallel to DC.Prove that Fis the mid-point of BC and $E F = \frac{1}{2} (A B + D C)$
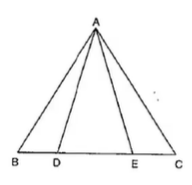
View Solution
In Figure, $A D = A E a n d D a n d E$ are points on $B C$ such that $B D = E C .$ Prove that $A B = A C$

View Solution
In Figure, $A C > A B a n d D$ is the point on $A C$ such that $A B = A D .$ Prove that $B C > C D$

View Solution
In $A B C, D$ is the mid-point of $B C a n d E D$ is the bisector of the $∠ A D B a n d E F$ is drawn parallel to $B C$ cutting $A C$ in $F$ . Prove that $∠ E D F$ is a right angle.
View Solution
Tangents AB and AC are drawn to a circle from a point A, such that $∠ B A C = 40^{\circ}$ . A chord CP is drawn parallel to BA. The measure of $∠ C B P$ is:
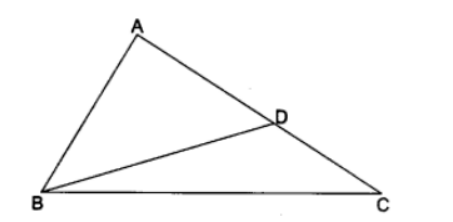
View Solution
In the given figure ,P is a point on the side BC of $△ A B C$ .Prove tat $(A B + B C + A C) G T 2 A P$
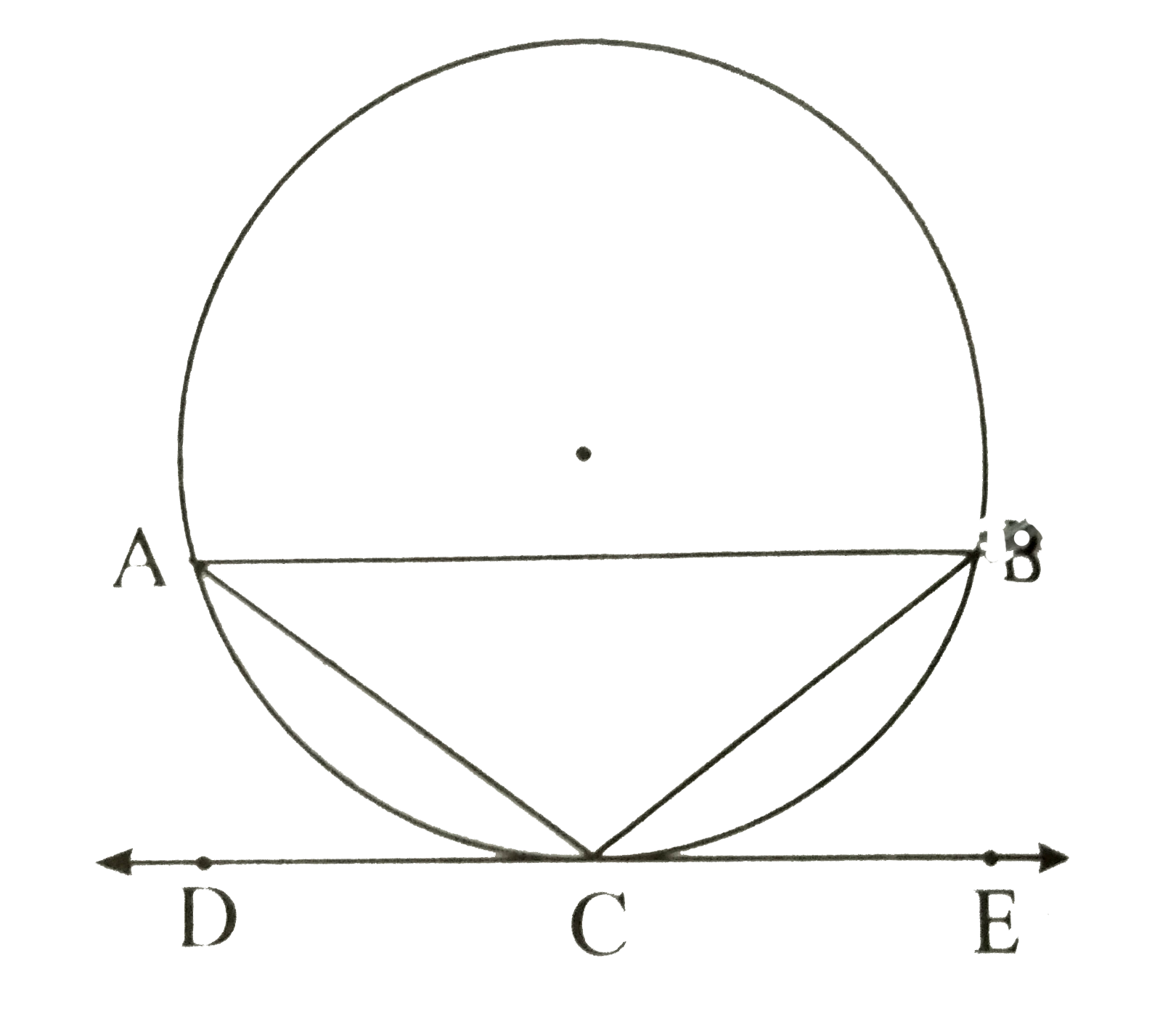
View Solution
In the figure, chord $A B ∣ ∣$ tangent DE. Tangent DE touches the circle at point C then prove AC = BC.

View Solution

CBSE COMPLEMENTARY MATERIAL-TRIANGLE-Short Answer Type Questions-II

In the given figure, DE || AC. Which of the following is correct? x=(...
02:24
Prove that the sum of the squares of the sides of a rhombus is equa...
05:22
A street light bulb is fixed on a pole 6 m above the level of the stre...
03:22
Two poles of height a metres and b metres are p metres apart. Prove th...
07:21
In the given figure AB || PQ || CD, AB=x, CD=y and PQ=z. Prove that 1/...
03:09
In the given figure (PS)/(SQ)=(PT)/(TR) and anglePST = anglePRQ. Prove...
03:50
In the figure, a point O inside triangleABC is joined to its vertices....
02:53
Two triangles B A Ca n dB D C , right angled at Aa n dD respectively, ...
02:17
The Hypotenuse of a right triangle is 25 cm and out of the remaining t...
03:40
In the given figure DE || AC and (BE)/(EC)=(BC)/(CP). Prove that DC |...
03:04
In a quadrilateral ABCD, angleB=90^(@) and AD^(2)= AB^(2) + BC^(2)+CD^...
02:05
In the given figure, DE || BC, DE= 3 cm, BC = 9 cm and ar (DADE) = 30c...
03:41
In an equilateral triangle ABC, D is a point on side BC such that B D=...
07:33
Ii DeltaPQR, PDbotQR such that D lies on QR, if PQ=a,PR=b,QD=c and DR=...
02:48
The ratio of the the areas of two similar triangles is equal to the ra...
07:50
In the given figure, the line segment XY is Parallel to AC of ΔABC and...
04:51
Through the vertex D of a parallelogram ABCD, a line is drawn to inter...
04:46
Theorem 6.9 : In a triangle, if square of one side is equal to the sum...
08:08
Prove that is a right angle triangle, the square of the hypotenuse is ...
04:40
Theorem 6.1 : If a line is drawn parallel to one side of a triangle to...
08:03

Home
Ask Doubt
Profile

In the figure, a point O inside △ABC is joined to its vertices. From a point D on AO, DE is drawn parallel to AB and from a point E on BO, EF is drawn parallel to BC. Prove that DF || AC.

Topper's Solved these Questions

Similar Questions

Knowledge Check

In ΔPQR, QR=10, RP=11 and PQ=12. D is the midpoint of PR, DE is drawn parallel to PQ meeting QR in E. EF is drawn parallel to RP meeting PQ in F. What is the length of DF?

CBSE COMPLEMENTARY MATERIAL-TRIANGLE-Short Answer Type Questions-II

In the figure, a point O inside $△ A B C$ is joined to its vertices. From a point D on AO, DE is drawn parallel to AB and from a point E on BO, EF is drawn parallel to BC. Prove that DF || AC.

In $Δ P Q R$ , QR=10, RP=11 and PQ=12. D is the midpoint of PR, DE is drawn parallel to PQ meeting QR in E. EF is drawn parallel to RP meeting PQ in F. What is the length of DF?