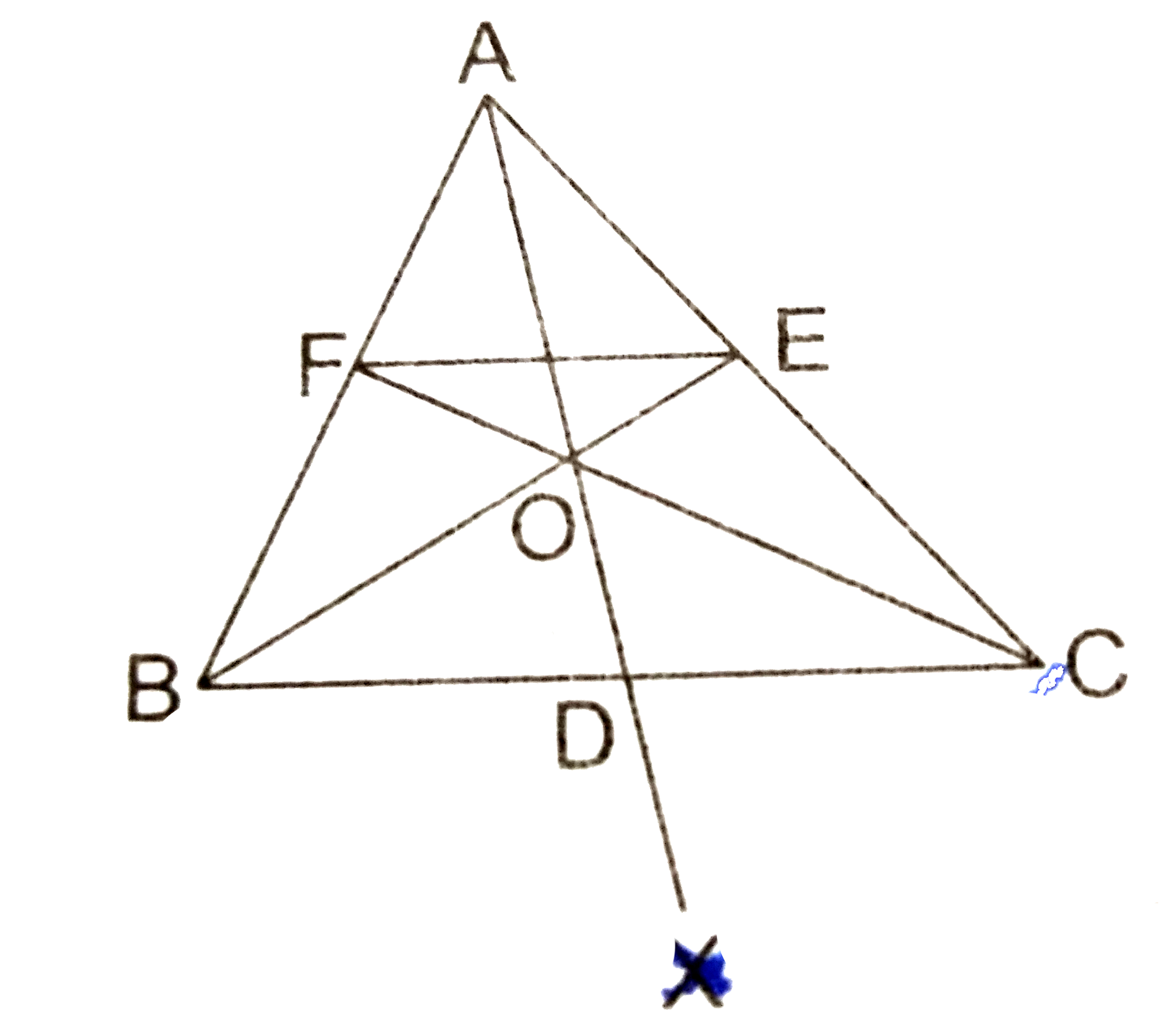
The side BC of a triangle ABC is bisected at D;o is any point in AD,BOandCO produced meet ACandAB in EandF respectively and AD is produced to X so that D is the mid-point of OX. Prove that AO:AX=AF:AB and show that FEBC.
To solve the problem, we will follow a structured approach to prove that AOAX=AFAB and that FE∥BC.
1. Identify the Given Information:
- Triangle ABC with D as the midpoint of side BC.
- Points O lies on line segments AD, BO, and CO extended, meeting AC and AB at points E and F respectively.
- AD is extended to X such that D is the midpoint of OX.
2. Establish Relationships:
- Since D is the midpoint of BC, we have BD=CD.
- Since D is also the midpoint of OX, we have OD=DX.
3. Use the Midpoint Theorem:
- From the midpoint theorem, since BD=CD and OD=DX, we can conclude that the segments BC and OX bisect each other.
- This implies that quadrilateral BCOX is a parallelogram because both pairs of opposite sides are equal.
4. Establish Parallel Lines:
- Since BCOX is a parallelogram, it follows that BO∥CX and BX∥CO.
5. Use Similar Triangles:
- In triangles ABX and AOC:
- Since BX∥CO, by the Basic Proportionality Theorem (Thales's theorem), we have:
AFAB=AOAX
6. Conclude the Ratios:
- Thus, we have established that:
AOAX=AFAB
7. Show that FE∥BC:
- Since AF and AE divide AB and AC in the same ratio, by the converse of the Basic Proportionality Theorem, we conclude that:
FE∥BC
Final Result:
We have proved that AOAX=AFAB and that FE∥BC.
- Triangle ABC with D as the midpoint of side BC.
- Points O lies on line segments AD, BO, and CO extended, meeting AC and AB at points E and F respectively.
- AD is extended to X such that D is the midpoint of OX.
- Since D is the midpoint of BC, we have BD=CD.
- Since D is also the midpoint of OX, we have OD=DX.
- From the midpoint theorem, since BD=CD and OD=DX, we can conclude that the segments BC and OX bisect each other.
- This implies that quadrilateral BCOX is a parallelogram because both pairs of opposite sides are equal.
- Since BCOX is a parallelogram, it follows that BO∥CX and BX∥CO.
- In triangles ABX and AOC:
- Since BX∥CO, by the Basic Proportionality Theorem (Thales's theorem), we have:
AFAB=AOAX
- Thus, we have established that:
AOAX=AFAB
- Since AF and AE divide AB and AC in the same ratio, by the converse of the Basic Proportionality Theorem, we conclude that:
FE∥BC
We have proved that AOAX=AFAB and that FE∥BC.
Topper's Solved these Questions
Similar Questions
The side BC of a triangle ABC is bisected at D;o is any point in AD,BOandCO produced meet ACandAB in EandF respectively and AD is produced to X so that D is the mid-point of OX. Prove that AO:AX=AF:AB and show that FEBC.
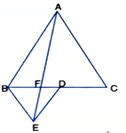
View SolutionThe side BC of a ΔABC is bisected at D. O is any point on AD, BO and CO are produced to meet AC and AB at E and F respectively and AD is produced to G so that D is the midpoint of OG. Prove that FE∣∣BC
View SolutionIn the given figure, side BC of ΔABC is bisected at D and O is any point AD.BO and CO produced meet AC and AB at E and F respectively, and AD is respectively, and AD is produced to X so that D is the midpoint of OX. Prove that AO:AX=AF:AB and show that EF∣∣BC.
 View Solution
View SolutionIn A ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (RQC)=38 ar ( ABC)
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that (i) ar(PRQ)=12ar(ARC)(ii) ar(RQC)=38ar(ABC)(iii) ar(PBQ)=ar(ARC)
View SolutionIn A ABC , P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar(PRQ)=12ar(ARC)
View SolutionABCD is a parallelogram. AD is a produced to E so that DE=DC and EC produced meets AB produced in F. Prove that BF=BC.
View SolutionABC is a triangle in which D is the mid-point of BC ,E andF are mid-points of DC and AE respectively. If area of ABC is 16cm2, find the area of DEF
View SolutionThe diagonals of a rectangle ABCD meet at O . If ∠BOC=44∘, find ∠OAD
View SolutionIn Figure, ABC and BDE are two equilateral triangls such that D is the mid-point of BC.AE intersects BC in F. Prove that: ar ( BFE)= 2 ar (EFD)
 View Solution
View Solution

