In a trapezium ABCD, AB || DC, AB = a cm, and DC = b cm. If M and N are the midpoints of the nonparallel sides, AD and BC respectively then find the ratio of ar(DCNM) and ar(MNBA).
The correct Answer is:(3a+b):(a+3b)
To find the ratio of the areas of trapeziums DCNM and MNBA in trapezium ABCD where AB || DC, AB = a cm, and DC = b cm, and M and N are midpoints of non-parallel sides AD and BC, we can follow these steps:
Step 1: Understand the trapezium and identify midpoints
In trapezium ABCD, we have:
- AB || DC
- AB = a cm
- DC = b cm
- M is the midpoint of AD
- N is the midpoint of BC
Step 2: Calculate the length of MN
Since M and N are midpoints, the length of MN can be calculated using the formula for the length of the segment connecting the midpoints of two sides of a trapezium:
MN=AB+DC2=a+b2
Step 3: Calculate the area of trapezium DCNM
The area of trapezium DCNM can be calculated using the formula for the area of a trapezium:
AreaDCNM=12×(DC+MN)×h
Where h is the height of the trapezium. Substituting the values we have:
AreaDCNM=12×(b+a+b2)×h
=12×(b+a+b2)×h
=12×(2b+a+b2)×h
=12×(a+3b2)×h
=(a+3b)h4
Step 4: Calculate the area of trapezium MNBA
Similarly, the area of trapezium MNBA can be calculated:
AreaMNBA=12×(MN+AB)×h
Substituting the values we have:
AreaMNBA=12×(a+b2+a)×h
=12×(a+b+2a2)×h
=12×(3a+b2)×h
=(3a+b)h4
Step 5: Find the ratio of the areas
Now, we can find the ratio of the areas of trapezium DCNM to trapezium MNBA:
Ratio=AreaDCNMAreaMNBA=(a+3b)h4(3a+b)h4
The h and 14 cancel out:
Ratio=a+3b3a+b
Final Answer
The ratio of the areas of trapezium DCNM to trapezium MNBA is:
a+3b3a+b
In trapezium ABCD, we have:
- AB || DC
- AB = a cm
- DC = b cm
- M is the midpoint of AD
- N is the midpoint of BC
Since M and N are midpoints, the length of MN can be calculated using the formula for the length of the segment connecting the midpoints of two sides of a trapezium:
MN=AB+DC2=a+b2
The area of trapezium DCNM can be calculated using the formula for the area of a trapezium:
AreaDCNM=12×(DC+MN)×h
Where h is the height of the trapezium. Substituting the values we have:
AreaDCNM=12×(b+a+b2)×h
=12×(b+a+b2)×h
=12×(2b+a+b2)×h
=12×(a+3b2)×h
=(a+3b)h4
Similarly, the area of trapezium MNBA can be calculated:
AreaMNBA=12×(MN+AB)×h
Substituting the values we have:
AreaMNBA=12×(a+b2+a)×h
=12×(a+b+2a2)×h
=12×(3a+b2)×h
=(3a+b)h4
Now, we can find the ratio of the areas of trapezium DCNM to trapezium MNBA:
Ratio=AreaDCNMAreaMNBA=(a+3b)h4(3a+b)h4
The h and 14 cancel out:
Ratio=a+3b3a+b
The ratio of the areas of trapezium DCNM to trapezium MNBA is:
a+3b3a+b
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)5videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (very Short Answer Questions)10videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )5videos
CIRCLE
Similar Questions
In figure, if DE||BC, then find the ratio of ar (ΔADE) and ar(DECB).
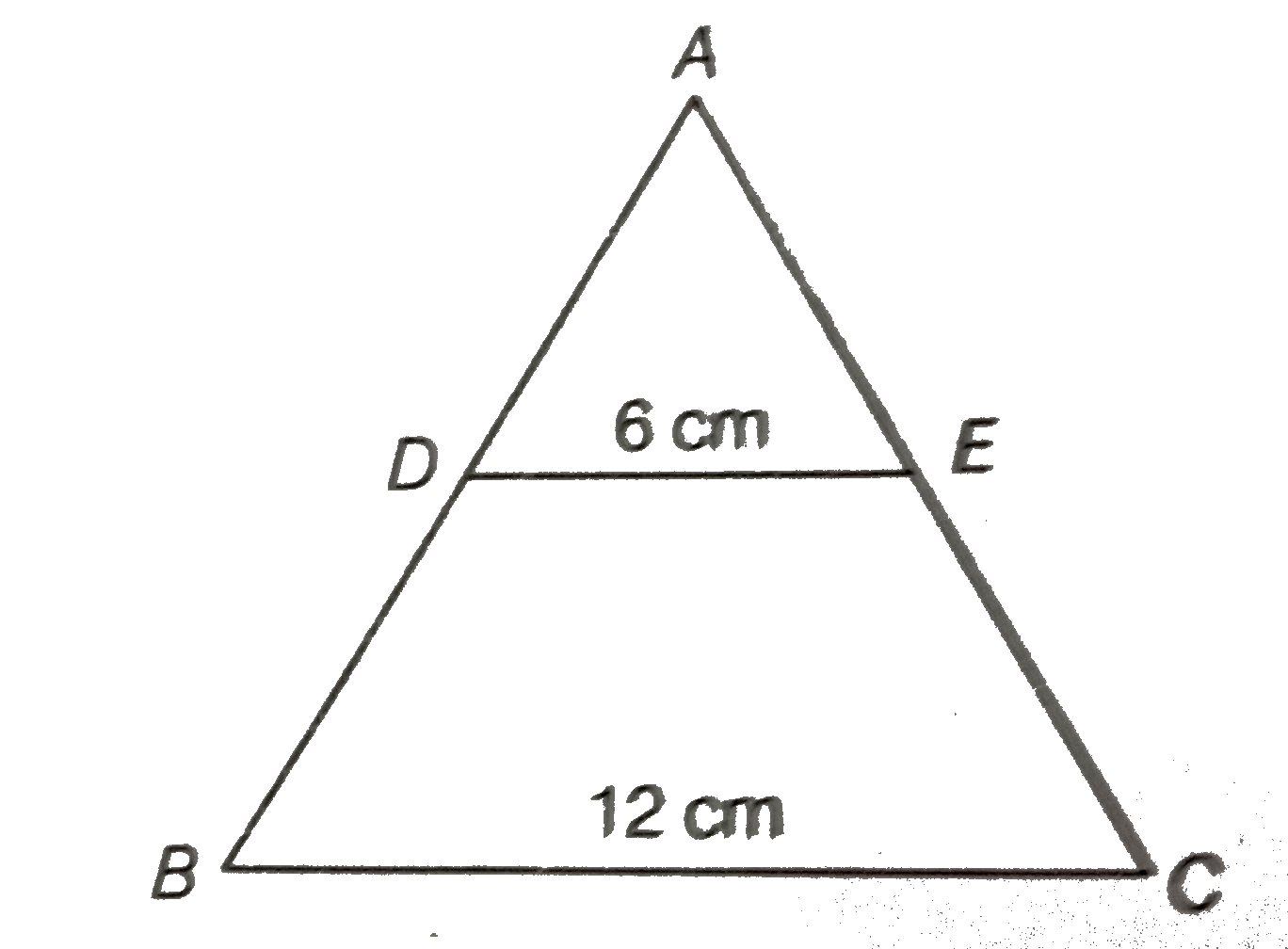 View Solution
View SolutionThe figure, given below, shows a trapezium ABCD. M and N are the mid-points of the nonparallel sides AD and BC respectively. Find:
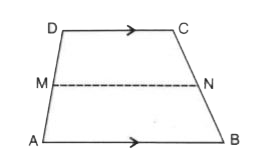
MN, if AB = 11 cm and DC = 8 cm.View SolutionThe figure, given below, shows a trapezium ABCD. M and N are the mid-points of the nonparallel sides AD and BC respectively. Find:
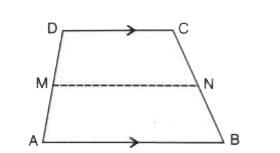
AB, if DC = 20 cm and MN = 27 cmView SolutionThe figure, given below, shows a trapezium ABCD. M and N are the mid-points of the nonparallel sides AD and BC respectively. Find:
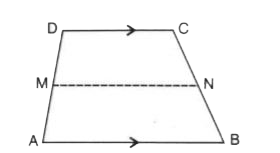
DC, if MN = 15 cm and AB = 23 cm.View SolutionABCD is a trapezium with AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB. Show thatAEED=BFFC.
View SolutionABCD is trapezium in which AB∣∣DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that
ar(DCYX)=79ar(XYBA).View SolutionIn trapezium ABCD, as shown, AB // DC, AD = DC = BC = 20 cm and ∠A=60∘. Find:
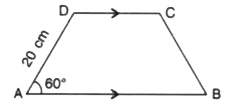
(i) length of ABView SolutionIn trapezium ABCD, AB is parallel to DC. P and Q are the mid-points of AD and BC respectively. BP produced meets CD produced at point E. Prove that :
PQ is parallel to AB.View SolutionIn trapezium ABCD, AB is parallel to DC. P and Q are the mid-points of AD and BC respectively. BP product meets CD produced at point E. Prove that :
Point P bisects BE,View SolutionIn trapezium ABCD, as shown, AB // DC, AD = DC = BC = 20 cm and ∠A=60∘. Find:
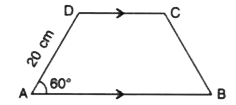
(ii) distance between AB and DC.View Solution
